Машина Поста

Одной из фундаментальных статей, результаты которой лежат в основе современной теории алгоритмов является статья Эмиля Поста (Emil Post), «Финитные комбинаторные процессы, формулировка 1», опубликованная в 1936 году в сентябрьском номере «Журнала символической логики»

Пост рассматривает общую проблему, состоящую из множества конкретных проблем, при этом решение общей проблемы это такое решение, которое доставляет ответ для каждой конкретной проблемы.

Например, решение уравнения 3х + 9 = 0 – это одна из конкретных проблем, а решение уравнения ax + b = 0 – это общая проблема, тем самым алгоритм (сам термин «алгоритм» не используется Постом) должен быть универсальным, т.е. должен быть соотнесен с общей проблемой.

Основные понятия алгоритмического формализма Поста – это пространство символов (язык L) в котором задаётся конкретная проблема и получается ответ, и набор инструкций, т.е. операций в пространстве символов, задающих как сами операции, так и порядок выполнения инструкций.

Машина Поста состоит из ленты и каретки (называемой также считывающей и записывающей головкой). Лента бесконечна и разделена на секции одинакового размера; для наглядности ленту считают расположенной горизонтально:

Лента бесконечна лишь для простоты изложения. Можно предположить, что лента не бесконечная, а лишь неограниченно растущая в обе стороны: например, можно считать, что лента наращивается на одну секцию, как только каретка доходит до конца ленты и должна двигаться дальше, или что за каждую единицу времени слева и справа нарастает по одной секции. Удобнее, однако, считать, что все секции слева и справа уже наросли, и тем самым, хотя и в ущерб реальности, полагать ленту бесконечной в обе стороны.

Порядок, в котором расположены секции ленты, подобен порядку, в котором расположены все целые числа. Поэтому естественно ввести на ленте «целочисленную систему координат», занумеровав секции целыми числами …-3, -2, -1, 0, 1, 2, 3, ….

Будем считать, что система координат жестко сопоставима с лентой, и получим таким образом возможность указывать какую-либо секцию ленты, называя ее порядковый номер, или координату.

В каждой секции ленты может быть либо ничего не записано (такая секция называется пустой), либо записана метка V (тогда секция называется отмеченной).

V

V

V

V

Информация о том, какие секции пусты, а какие отмечены, образует состояние ленты. Иными словами, состояние ленты – это функция, которая каждому числу (номеру секции) ставит в соответствие либо метку, либо пустой символ. Состояние ленты меняется в процессе работы.

Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит ровно против одной секции ленты. Говорят, что каретка обозревает эту секцию, или держит ее в поле зрения.

Информация о том, какие секции пусты, а какие отмечены и где стоит каретка, образует состояние машины Поста. Таким образом, состояние машины слагается из состояния ленты и указания номера той секции, которую обозревает каретка. За единицу времени (которую называют шагом) каретка может сдвинуться на одну секцию влево или вправо. Кроме того, каретка может поставить (напечатать) или уничтожить (стереть) метку в той секции, против которой она стоит, а также распознать, стоит или нет метка в обозреваемой ею секции.

Работа машины Поста состоит в том, что каретка передвигается вдоль ленты и печатает или стирает метки. Эта работа происходит по инструкции определенного вида, называемой программой.

Каждая программа машины Поста состоит из команд. Командой машины Поста будем называть выражение, имеющее один из следующих шести видов ():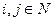

№ п/п	Название	Обозначение	Действие
	Команды движения вправо		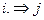каретка сдвигается на одну секцию вправо
	Команды движения влево		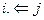каретка сдвигается на одну секцию влево
	Команды печатания метк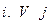и	; или	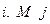каретка печатает метку на обозреваемой секции (выполнение этой команды возможно лишь в том случае, если обозреваемая перед началом выполнения команды секция пуста, в противном случае команда считается невыполнимой)
	Команды стирания метк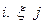и	или	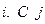каретка стирает метку в обозреваемой секции (выполнение этой команды возможно лишь в том случае, если обозреваемая секция отмечена, в противном случае команда считается невыполнимой)
	Команды передачи управления	i.? j1, j2	если секция, обозреваемая перед началом выполнения команды, была пуста, то следующей должна выполняться команда с номером j1, если же эта секция была отмечена, следующей должна выполняться команда с номером j2; состояние ленты при этом не изменяется
	Команды остановки	i. стоп	машина останавливается

Например, 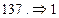является командой движения вправо, 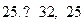– командой передачи управления.

Число i, стоящее в начале команды, называется номером команды. Число j, стоящее в конце команды (а у команд передачи управления – каждое из чисел j₁ и j₂), будем называть отсылкой (при этом в команде передачи управления j₁ – верхней, а j₂ – нижней отсылкой).

Программой машины Поста будем называть конечный непустой (т.е. содержащий хотя бы одну команду) список команд машины Поста, обладающий следующими двумя свойствами:

1) На первом месте в этом списке стоит команда с номером 1, на втором месте (если оно есть) – команда с номером 2 и т.д.; вообще на k -м месте стоит команда с номером k.

2) Отсылка любой из команд списка совпадает с номером некоторой (другой или той же самой) команды списка (более точно: для каждой отсылки каждой команды списка найдется в списке такая команда, номер которой равен рассматриваемой отсылке).

Например, следующий список будет программой машины Поста:

1. стоп

2.? 4, 1

3. С 3

4. стоп

А эти два списка не будут программами машины Поста, хотя и составлены из команд машины Поста:

2.? 4, 1 1. стоп

1. стоп 2.? 4, 5

3. С 3 3. С 3

4. стоп 4. стоп

(не выполнено первое условие); (не выполнено второе условие).

Как правило, программы машины Поста записывают в столбик. Число команд программы называется длиной программы.

Чтобы машина Поста начала работать, надо задать, во-первых, некоторую программу, а во-вторых, некоторое ее (машины) состояние, т.е. как-то расставить метки по секциям ленты (в частности, можно все секции оставить пустыми) и поставить каретку против одной из секций. Если секции пронумерованы, то предполагается, что в начальном состоянии (т.е. задаваемом вначале) машины каретка ставится всегда против секции с номером (координатой) нуль. При таком соглашении начальное состояние машины полностью определено состоянием ленты.

Программа является той инструкцией, на основании которой работает машина. Работа машины на основании заданной программы (и при заданном начальном состоянии) происходит следующим образом. Машина приводится в начальное состояние и приступает к выполнению первой команды программы. Эта команда выполняется за один шаг, после чего машина приступает к выполнению той команды (назовем его a), номер которой равен отсылке (одной из отсылок, если их две) первой команды. Эта команда также выполняется за один шаг, после чего начинается выполнение команды, номер которой равен отсылке команды с номером a. Вообще каждая команда выполняется за один шаг, а переход от выполнения одной команды к выполнению другой происходит по следующему правилу: пусть на k -м шаге выполнялась команда с номером i, тогда, если эта команда имеет единственную отсылку j, то на k+1 -м шаге выполняется команда с номером j. Если эта команда имеет две отсылки j₁ и j₂, то на k+1 -м шаге выполняется одна из двух команд – с номером j₁ или с номером j₂ в соответствии с состоянием обозреваемой ячейки. Если, наконец, выполняющаяся на k -м шаге команда вовсе не имеет отсылки, то на k+1 -м шаге и на всех последующих шагах не выполняется никакая команда: машина останавливается.

Если теперь, задавшись программой и каким-либо начальным состоянием, пустить машину в ход, то осуществится один из следующих вариантов:

1) В ходе выполнения программы машина дойдет до выполнения невыполнимой команды (печатания метки в непустой секции или стирания метки в пустой секции); выполнение программы тогда прекращается, машина останавливается; происходит так называемая безрезультатная остановка.

2) В ходе выполнения программы машина дойдет до выполнения команды остановки; программа в этом случае считается выполненной, машина останавливается; происходит так называемая результативная остановка.

3) В ходе выполнения программы машина не дойдет до выполнения ни одной из команд, указанных в первых двух вариантах; выполнение программы при этом никогда не прекращается, машина никогда не останавливается; процесс работы машины происходит бесконечно.

Дата добавления: 2014-01-06