Лекция по нейронным сетям

Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.

В общем случае механизм логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация (см. рисунок 5).

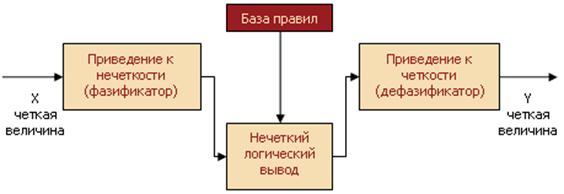
Рисунок 5. Система нечеткого логического вывода.

Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.

1. Как работает биологическая нейронная сеть

Нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений от нашей кожи, ушей и глаз к мозгу, процессы мышления и управления действиями - все это реализовано в живом организме как передача электрических импульсов между нейронами. Рассмотрим строение биологического нейрона.

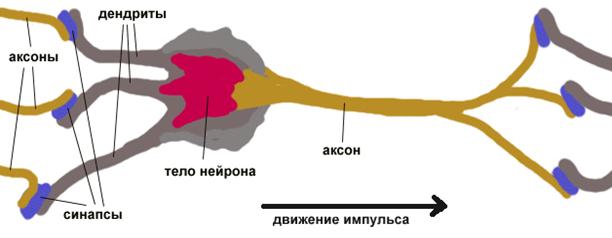Каждый нейрон имеет отростки нервных волокон двух типов - дендриты, по которым принимаются импульсы, и единственный аксон, по которому нейрон может передавать импульс. Аксон контактирует с дендритами других нейронов через специальные образования - синапсы, которые влияют на силу импульса.

Можно считать, что при прохождении синапса сила импульса меняется в определенное число раз, которое мы будем называть весом синапса. Импульсы, поступившие к нейрону одновременно по нескольким дендритам, суммируются. Если суммарный импульс превышает некоторый порог, нейрон возбуждается, формирует собственный импульс и передает его далее по аксону. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующего нейрона.

Нетрудно построить математическую модель описанного процесса.

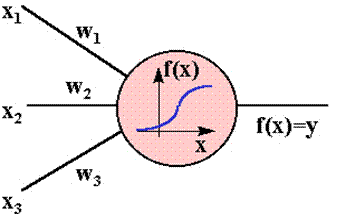
На рисунке изображена модель нейрона с тремя входами (дендритами), причем синапсы этих дендритов имеют веса w₁, w₂, w₃. Пусть к синапсам поступают импульсы силы x₁, x₂, x₃ соответственно, тогда после прохождения синапсов и дендритов к нейрону поступают импульсы w₁x₁, w₂x₂, w₃x₃. Нейрон преобразует полученный суммарный импульс x=w₁x₁+ w₂x₂+ w₃x₃ в соответствии с некоторой передаточной функцией f(x). Сила выходного импульса равна y=f(x)=f(w₁x₁+ w₂x₂+ w₃x₃).

Таким образом, нейрон полностью описывается своими весами w_k и передаточной функцией f(x). Получив набор чисел (вектор) x_k в качестве входов, нейрон выдает некоторое число y на выходе.

2. Что такое искусственная нейронная сеть

Иску́сственные нейро́нные се́ти (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети Маккалока и Питтса [1]. Впоследствии, после разработки алгоритмов обучения, получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.

ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов).

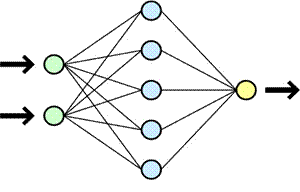
Такие процессоры обычно довольно просты, особенно в сравнении с процессорами, используемыми в персональных компьютерах. Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые процессоры вместе способны выполнять довольно сложные задачи.

С точки зрения машинного обучения, нейронная сеть представляет собой частный случай методов распознавания образов, дискриминантного анализа, методов кластеризации и т. п. С математической точки зрения, обучение нейронных сетей — это многопараметрическая задача нелинейной оптимизации. С точки зрения кибернетики, нейронная сеть используется в задачах адаптивного управления и как алгоритмы для робототехники. С точки зрения развития вычислительной техники и программирования, нейронная сеть — способ решения проблемы эффективного параллелизма[2]. А с точки зрения искусственного интеллекта, ИНС является основой философского течения коннективизма и основным направлением в структурном подходе по изучению возможности построения (моделирования) естественного интеллекта с помощью компьютерных алгоритмов.

Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что в случае успешного обучения сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке, а также неполных и/или «зашумленных», частично искаженных данных.

Как работает нейронная сеть

Искусственная нейронная сеть (ИНС, нейронная сеть) - это набор нейронов, соединенных между собой. Как правило, передаточные функции всех нейронов в нейронной сети фиксированы, а веса являются параметрами нейронной сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы нейронной сети, а некоторые выходы - как внешние выходы нейронной сети. Подавая любые числа на входы нейронной сети, мы получаем какой-то набор чисел на выходах нейронной сети. Таким образом, работа нейронной сети состоит в преобразовании входного вектора в выходной вектор, причем это преобразование задается весами нейронной сети.

Практически любую задачу можно свести к задаче, решаемой нейронной сетью. В этой таблице показано, каким образом следует сформулировать в терминах нейронной сети задачу распознавания рукописных букв.

Задача распознавания рукописных букв

Дано: растровое черно-белое изображение буквы размером 30x30 пикселов

Надо: определить, какая это буква (в алфавите 33 буквы)

Формулировка для нейронной сети:

Дано: входной вектор из 900 двоичных символов (900=30x30)

Надо: построить нейронную сеть с 900 входами и 33 выходами, которые помечены буквами. Если на входе нейронной сети изображение буквы "А", то максимальное значение выходного сигнала достигается на выходе "А". Аналогично нейронная сеть работает для всех 33 букв.

Поясним, зачем требуется выбирать выход нейронной сети с максимальным уровнем сигнала. Дело в том, что уровень выходного сигнала, как правило, может принимать любые значения из какого-то отрезка. Однако, в данной задаче нас интересует не аналоговый ответ, а всего лишь номер категории (номер буквы в алфавите). Поэтому используется следующий подход - каждой категории сопоставляется свой выход, а ответом нейронной сети считается та категория, на чьем выходе уровень сигнала максимален. В определенном смысле уровень сигнала на выходе "А" - это достоверность того, что на вход нейронной сети была подана рукописная буква "A". Задачи, в которых нужно отнести входные данные к одной из известных категорий, называются задачами классификации. Изложенный подход - стандартный способ классификации с помощью нейронных сетей.

Как постороить нейронную сеть

Теперь, когда стало ясно, что именно мы хотим построить, мы можем переходить к вопросу "как строить такую нейронную сеть". Этот вопрос решается в два этапа:

1. Выбор типа (архитектуры) нейронной сети.

2. Подбор весов (обучение) нейронной сети.

На первом этапе следует выбрать следующее:

какие нейроны мы хотим использовать (число входов, передаточные функции);

каким образом следует соединить их между собой;

что взять в качестве входов и выходов нейронной сети.

Эта задача на первый взгляд кажется необозримой, но, к счастью, нам необязательно придумывать нейронную сеть "с нуля" - существует несколько десятков различных нейросетевых архитектур, причем эффективность многих из них доказана математически. Наиболее популярные и изученные архитектуры - это многослойный перцептрон, нейронная сеть с общей регрессией, нейронные сети Кохонена и другие.

На втором этапе нам следует "обучить" выбранную нейронную сеть, то есть подобрать такие значения ее весов, чтобы она работала нужным образом. Необученная нейронная сеть подобна ребенку - ее можно научить чему угодно. В используемых на практике нейронных сетях количество весов может составлять несколько десятков тысяч, поэтому обучение - действительно сложный процесс. Для многих архитектур разработаны специальные алгоритмы обучения, которые позволяют настроить веса нейронной сети определенным образом. Наиболее популярный из этих алгоритмов - метод обратного распространения ошибки (Error Back Propagation), используемый, например, для обучения перцептрона.

Обучение нейронных сетей

Обучить нейронную сеть - значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку изображение буквы "А", мы спрашиваем его: "Какая это буква?" Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: "Это буква А". Ребенок запоминает этот пример вместе с верным ответом, то есть в его памяти происходят некоторые изменения в нужном направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все 33 буквы будут твердо запомнены. Такой процесс называют "обучение с учителем".

При обучении нейронной сети мы действуем совершенно аналогично. У нас имеется некоторая база данных, содержащая примеры (набор рукописных изображений букв). Предъявляя изображение буквы "А" на вход нейронной сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен и верный (желаемый) ответ - в данном случае нам хотелось бы, чтобы на выходе нейронной сети с меткой "А" уровень сигнала был максимален. Обычно в качестве желаемого выхода в задаче классификации берут набор (1, 0, 0,...), где 1 стоит на выходе с меткой "А", а 0 - на всех остальных выходах. Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем 33 числа - вектор ошибки. Алгоритм обратного распространения ошибки - это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов нейронной сети. Одну и ту же букву (а также различные изображения одной и той же буквы) мы можем предъявлять нейронной сети много раз. В этом смысле обучение скорее напоминает повторение упражнений в спорте - тренировку.

Оказывается, что после многократного предъявления примеров веса нейронной сети стабилизируются, причем нейронная сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что "нейронная сеть выучила все примеры", "нейронная сеть обучена", или "нейронная сеть натренирована". В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную нейронную сеть считают натренированной и готовой к применению на новых данных.

Важно отметить, что вся информация, которую нейронная сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения нейронной сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать нейронную сеть для предсказания финансового кризиса, если в обучающей выборке кризисов не представлено. Считается, что для полноценной тренировки нейронной сети требуется хотя бы несколько десятков (а лучше сотен) примеров.

Повторим еще раз, что обучение нейронных сетей - сложный и наукоемкий процесс. Алгоритмы обучения нейронных сетей имеют различные параметры и настройки, для управления которыми требуется понимание их влияния.

Применение нейронной сети

После того, как нейронная сеть обучена, мы можем применять ее для решения полезных задач. Важнейшая особенность человеческого мозга состоит в том, что, однажды обучившись определенному процессу, он может верно действовать и в тех ситуациях, в которых он не бывал в процессе обучения. Например, мы можем читать почти любой почерк, даже если видим его первый раз в жизни. Так же и нейронная сеть, грамотным образом обученная, может с большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Например, мы можем нарисовать букву "А" другим почерком, а затем предложить нашей нейронной сети классифицировать новое изображение. Веса обученной нейронной сети хранят достаточно много информации о сходстве и различиях букв, поэтому можно рассчитывать на правильный ответ и для нового варианта изображения.

Дата добавления: 2014-01-06