Взаимное положение прямой и плоскости, двух плоскостей

Взаимное положение прямой и плоскости определяется количествомобщих точек:

1) если прямая имеет две общие точки с плоскостью, то она принадлежит этой плоскости,

2) если прямая имеет одну общую точку с плоскостью, то прямая пересекает плоскость,

3) если точка пересечения прямой с плоскостью удалена в бесконечность, то прямая и плоскость параллельны.

Задачи, в которых определяется взаимное расположение различных геометрических фигур относительно друг друга, называются позиционными задачами.

Прямая принадлежащая плоскости рассматривалась ранее.

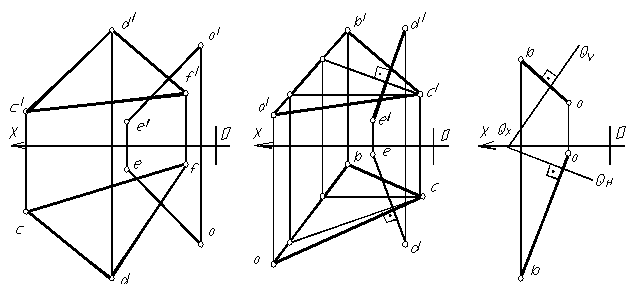
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости. Чтобы построить такую прямую, необходимо в плоскости задать любую прямую и параллельно ей провести требуемую.

Рис. 1.53 Рис. 1.54 Рис.1.55

Пусть через точку А (рис. 1.53) необходимо провести прямую АВ, параллельную плоскости Q, заданную треугольником CDF. Для этого через фронтальную проекцию точки а ^/ точки А проведем фронтальную проекцию а^/в^/ искомой прямой параллельно фронтальной проекции любой прямой, лежащей в плоскости Р, например, прямой CD (а^/в^/!! с^/д^/). Через горизонтальную проекцию а точки А параллельно сд проводим горизонтальную проекцию ав искомой прямой АВ (ав11 сд). Прямая АВ параллельна плоскости Р, заданной треугольником CDF.

Из всех возможных положений прямой, пересекающей плоскость, отметим случай, когда прямая перпендикулярна плоскости. Рассмотрим свойства проекций такой прямой.

Рис. 1.56 Рис. 1.57

Прямая перпендикулярна плоскости (частный случай пересечения прямой с плоскостью) если она перпендикулярна какой-либо прямой, лежащей в плоскости. Для построения проекций перпендикуляра к плоскости, находящейся в общем положении, этого недостаточно без преобразования проекций. Поэтому вводят дополнительное условие: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся главным линиям (для построения проекций используется условие проецирования прямого угла). В этом случае: горизонтальная и фронтальная проекции перпендикуляра перпендикулярны соответственно горизонтальной проекции горизонтали и фронтальной проекции фронтали данной плоскости общего положения (рис. 1.54). При задании плоскости следами проекции перпендикуляра перпендикулярны соответственно фронтальная – фронтальному следу, горизонтальная – горизонтальному следу плоскости (рис. 1.55).

Пересечение прямой с проецирующей плоскостью. Рассмотрим прямую, пересекающую плоскость, когда плоскость находится в частном положении.

Плоскость, перпендикулярная плоскости проекций (проецирующая плоскость), проецируется на нее в виде прямой линии. На этой прямой (проекции плоскости) должна находиться соответствующая проекция точки, в которой некоторая прямая пересекает эту плоскость (рис.1.56).

На рисунке 1.56 фронтальная проекция точки К пересечения прямой АВ с треугольником СDE определяется в пересечении их фронтальных проекций, т.к. треугольник СDE проецируется на фронтальную плоскость в виде прямой линии. Находим горизонтальную проекцию точки пересечения прямой с плоскостью (она лежит на горизонтальной проекции прямой). Способом конкурирующих точек, определяем видимость прямой АВ относительно плоскости треугольника СDE на горизонтальной плоскости проекций.

На рисунке 1.59 изображена горизонтально-проецирующая плоскость P и прямая общего положения АВ. Т.к. плоскость Р перпендикулярна горизонтальной плоскости проекций, то все, что в ней находится, на горизонтальную плоскость проекций проецируется на ее след, в том числе и точка ее пересечения с прямой АВ. Следовательно, на комплексном чертеже имеем горизонтальную проекцию точки пересечения прямой с плоскостью Р. По принадлежности точки прямой, находим фронтальную проекцию точки пересечения прямой АВ с плоскость Р. Определяем видимость прямой на фронтальной плоскости проекций.

Рис. 1.58 Рис. 1.59

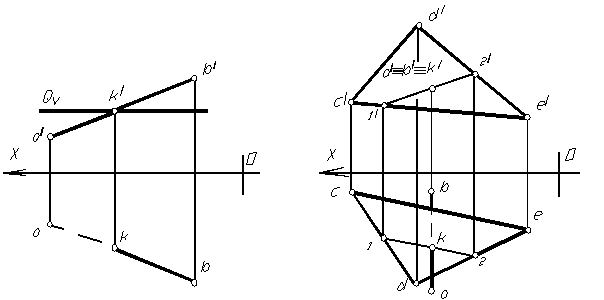
На рисунке 1.58 дан комплексный чертеж построения проекций точки пересечения прямой АВ с плоскостью горизонтального уровня G. Фронтальный след плоскости G является ее фронтальной проекцией. Фронтальная проекция точки пересечения плоскости G с прямой АВ определятся в пересечении фронтальной проекции прямой и фронтального следа плоскости. Имея фронтальную проекцию точки пересечения, находим горизонтальную проекцию точки пересечения прямой АВ с плоскостью G.

На рисунке 1.57 изображена плоскость общего положения, заданная треугольником CDE и фронтально-проецирующая прямая АВ? пересекающая плоскость в точке K. Фронтальная проекция точки – k^/ совпадает с точками a^/ и b ^/. Для построения горизонтальной проекции точки пересечения проведем через точку K в плоскости CDE прямую (например, 1-2). Построим ее фронтальную проекцию, а затем горизонтальную. Точка K является точкой пересечения прямых AB и 1-2. То есть точка K одновременно принадлежит прямой AB и плоскости треугольника и, следовательно, является точкой их пересечения.

Пересечение двух плоскостей. Прямая линия пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плоскостям, или одной точкой, принадлежащей двум плоскостям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух плоскостей.

Пересечение проецирующих плоскостей. Две плоскости могут быть параллельны между собой или пересекаться. Рассмотрим случаи взаимного пересечения плоскостей.

Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям, следовательно, необходимо и достаточно найти эти две точки, принадлежащей линии пересечения двух заданных плоскостей.

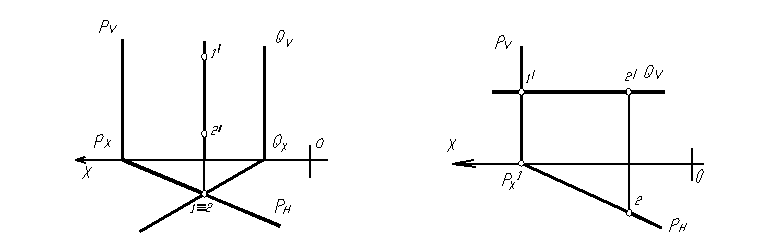
Следовательно, в общем случае для построения линии пересечения двух плоскостей необходимо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям. Эти точки и определяют линию пересечения плоскостей. Для нахождения каждой из этих двух точек обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна (или параллельна) к какой-либо плоскости проекций, то построение проекции линии их пересечения упрощается.

Рис. 1.60 Рис. 1.61

Если плоскости, заданны следами, то естественно искать точки, определяющие прямую пересечения плоскостей, в точках пересечения одноименных следов плоскостей попарно: прямая, проходящая через эти точки, является общей для обеих плоскостей, т.е. их линией пересечения.

Рассмотрим частные случаи расположения одной (или обеих) из пересекающихся плоскостей.

На комплексном чертеже (рис.1.60) изображены горизонтально-проецирующие плоскости P и Q. Тогда горизонтальная проекция их линии пересечения вырождается в точку, а фронтальная проекция – в прямую, перпендикулярную оси оx.

На комплексном чертеже (рис. 1.61) изображены плоскости частного положения: плоскость Р перпендикулярна горизонтальной плоскости проекций (горизонтально-проецирующая плоскость) и плоскость Q - плоскость горизонтального уровня. В этом случая, горизонтальная проекция их линии пересечения совпадет с горизонтальным следом плоскости Р, а фронтальная – с фронтальным следом плоскости Q.

В случае задания плоскостей следами легко установить, что эти плоскости пересекаются: если хотя бы одна пара одноименных следов пересекается, то плоскости пересекаются между собой.

Изложенное относится к плоскостям, заданных пересекающимися следами. Если же обе плоскости имеют на горизонтальной и фронтальной плоскостях следы, параллельные друг другу, то эти плоскости могут быть параллельны либо пересекаться. О взаимном положении таких плоскостей можно судить, построив третью проекцию (третий след). Если следы обеих плоскостей на третьей проекции так же параллельны, то плоскости параллельны между собой. Если следы на третьей плоскости пересекаются, то заданные в пространстве плоскости пересекаются.

Рис. 1.62

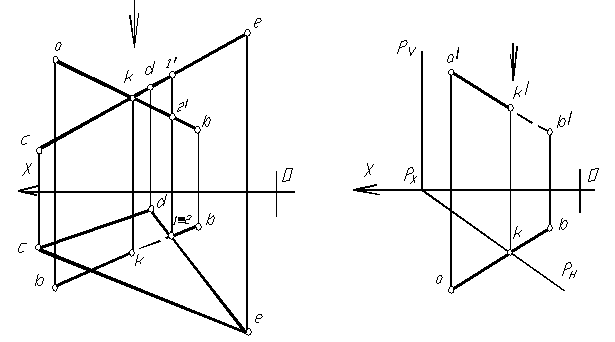
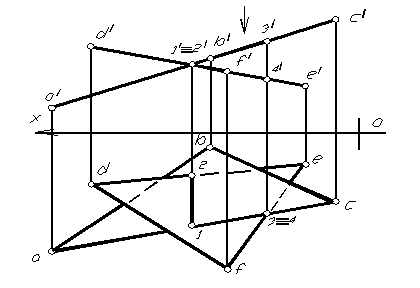
На комплексном чертеже (рис.1.62) изображены фронтально-проецирующие плоскости, заданные треугольником АВС и DEF. Проекция линии пересечения на фронтальной плоскости проекций – точка, т.е. так как треугольники перпендикулярны фронтальной плоскости проекций, то и их линия пересечения так же перпендикулярна фронтальной плоскости проекций. Следовательно горизонтальная проекции линии пересечения треугольников (12) перпендикулярна оси оx. Видимость элементов треугольников на горизонтальной плоскости проекции определяется с помощью конкурирующих точек (3,4).

На комплексном чертеже (рис. 1.63) заданы две плоскости: одна из которых треугольником АВС общего положения, другая – треугольником DEF перпендикулярна фронтальной плоскости проекций, т.е. находящийся в частном положении (фронтально-проецирующий). Фронтальная проекция линии пересечения треугольников (1^/ 2^/) находится исходя из общих точек, одновременно принадлежащих обоим треугольникам (все, что находится во фронтально- проецирующем треугольнике DEF на фронтальной проекции выльется в линию – проекцию его на фронтальную плоскость, в том числе и линия его пересечения с треугольником АВС. По принадлежности точек пересечения сторонам треугольника АВС, находим горизонтальную проекцию линии пересечения треугольников. Способом конкурирующих точек определяем видимость элементов треугольников на горизонтальной плоскости проекций.

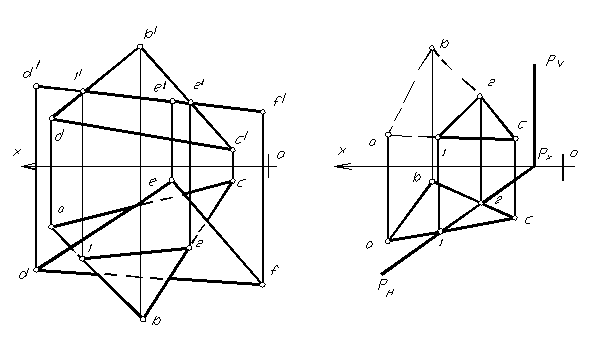Рис. 1.63 Рис. 1.64

На рисунке 1.64 дан комплексный чертеж двух плоскостей, заданных треугольником общего положения АВС и горизонтально-проецирующая плоскость Р, заданная следами. Так как плоскость Р – горизонтально- проецирующая, то все, что в ней находится, в том числе и линия ее пересечения с плоскостью треугольника АВС, на горизонтальной проекции совпадет с ее

горизонтальным следом. Фронтальную проекцию линии пересечения данных плоскостей находим из условия принадлежности точек элемента (сторонам) плоскости общего положения.

В случае задания плоскостей общего положения не следами, то для получения линии пересечения плоскостей последовательно находится точка встречи стороны одного треугольника с плоскостью другого треугольника. Если плоскости общего положения заданы не треугольниками, то линию ппересечения таких плоскостей можно найти путем введения поочередно двух вспомогательных секущих плоскостей – проецирующих (для задания плоскостей треугольниками) или уровня для всех других случаев.

Пересечение прямой общего положения с плоскость общего положения. Ранее были рассмотрены случаи пересечения плоскостей, когда одна из них являлась проецирующей. На основе этого мы можем найти точку пересечения прямой общего положения с плоскостью общего положения, путем введения дополнительной проецирующей плоскости-посредника.

Прежде чем рассматривать пересечение плоскостей общего положения, рассмотрим пересечение прямой общего положения с плоскостью общего положения.

Для нахождения точки встречи прямой общего положения с плоскостью общего положения необходимо:

1) прямую заключить во вспомогательную проецирующую плоскость,

2) найти линию пересечения заданной и вспомогательных плоскостей,

3)

определить общую точку, принадлежащую одновременно двум плоскостям (это их линия пересечения) и прямой.

Рис. 1.65 Рис. 1.66

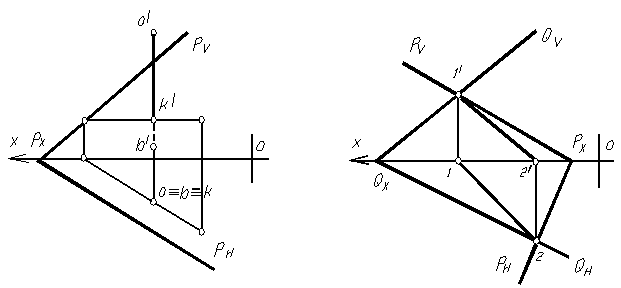
Рис. 1.67 Рис. 1.68

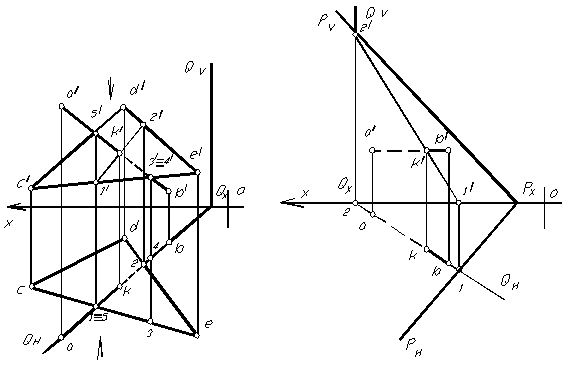
На комплексном чертеже (рис. 1.65) изображен треугольник СDE общего положения и прямая АВ общего положения. Для нахождения точки пересечения прямой с плоскостью, заключим прямую АВ во фронтально- проецирующую плоскость Q. Найдем линию пересечения (12) плоскости- посредника Q и заданной плоскости СDE. При построении горизонтально проекции линии пересечения найдется общая точка К, одновременно принадлежащая двум плоскостям и заданной прямой АВ. Из принадлежности точки прямой находим фронтальную проекцию точки пересечения прямой с заданной плоскостью. Видимость элементов прямой на плоскостях проекций, определяем с помощью конкурирующих точек.

На рисунке 1.66 показан пример нахождения точки встречи прямой АВ, являющейся горизонталью (прямая параллельна горизонтальной плоскости проекций) и плоскости Р, общего положения, заданной следами. Для нахождения точки их пересечения, прямая АВ заключается в горизонтально- проецирующую плоскость Q. Далее поступают, как и в выше изложенном примере.

Для нахождения точки встречи горизонтально-проецирующей прямой АВ с плоскостью общего положения (рис. 1.67), через точку встречи прямой с плоскостью (ее горизонтальная проекция совпадает с горизонтальной проекцией самой прямой) проводим горизонталь (т.е. привязываем точку пересечения прямой с плоскостью в плоскость Р). Найдя фронтальную проекцию проведенной горизонтали в плоскости Р, отмечаем фронтальную проекцию точки встречи прямой АВ с плоскостью Р.

Рис. 1.69

Для нахождения линии пересечения плоскостей общего положения, заданных следами достаточно отметить две общие точки, одновременно принадлежащие обеим плоскостям. Такими точками являются точки пересечения их следов (рис.1.68).

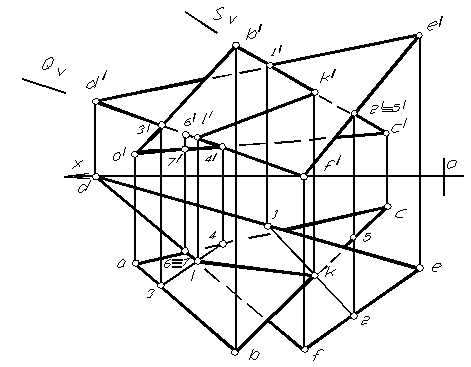
Для нахождения линии пересечения плоскостей общего положения, заданных двумя треугольниками (рис. 1.69), последовательно находим точку

встречи стороны одного треугольника с плоскостью другого треугольника. Взяв любые две стороны из любого треугольника, заключив их в проецирующие плоскости посредники, находятся две точки, одновременно принадлежащие обоим треугольникам – линия их пересечения.

На рисунке 1.69 дан комплексный чертеж треугольников ABC и DEF общего положения. Для нахождения линии пересечения данных плоскостей:

1. Заключаем сторону ВС треугольника АВС во фронтально- проецирующую плоскость S (выбор плоскостей совершенно произвольный).

2. Находим линию пересечения плоскости S и плоскости DEF – 12.

3. Отмечаем горизонтальную проекцию точки встречи (общая точка двух треугольников) К из пересечения 12 и ВС и находим ее фронтальную проекцию на фронтальной проекции прямой ВС.

4. Проводим вторую вспомогательную проецирующую плоскость Q через сторону DF треугольника DEF.

5. Находим линию пересечения плоскости Q и треугольника АВС – 3 4.

6. Отмечаем горизонтальную проекцию точки L, являющейся точкой встречи стороны DF c плоскостью треугольника АВС и находим ее фронтальную проекцию.

7. Соединяем одноименные проекции точек К и L. К L – линя пересечения плоскостей общего положения, заданных треугольниками АВС и DEF.

8. Способом конкурирующих точек определяем видимость элементов треугольников на плоскостях проекций.

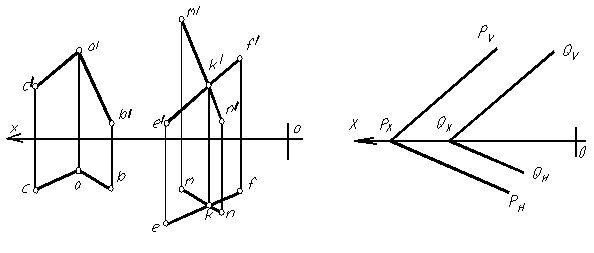Параллельные плоскости. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

Рис. 1.70 Рис. 1.71

На рисунке 1.70 построена плоскость, проходящая через точку К параллельная плоскости, заданной пересекающимися прямыми АВ и АС.

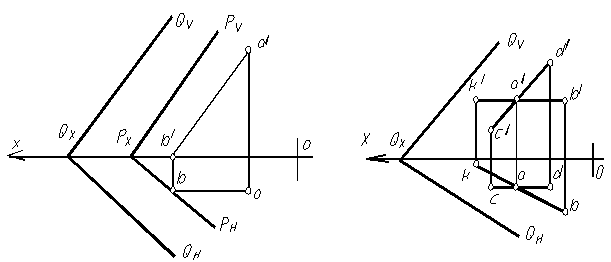Так как выше изложенное действительно и для главных линий параллельных плоскостей, то можно сказать, что плоскости параллельны, если параллельны их одноименные следы (рис. 1.71).

Рис. 1.72

На рисунке 1.72 показано построение плоскости параллельной заданной и проходящей через точку А. В первом случае через точку А проведена прямая (фронталь), параллельная заданной плоскости G. Тем самым проведена плоскость Р содержащая прямую параллельную заданной плоскости G и параллельная ей. Во втором случае через точку А проведена плоскость, заданная главными линиями из условия параллельности этих линий заданной плоскости G.

Рис. 1.73

Взаимно-перпендикулярные плоскости. Если одна плоскость содержит

хотя бы одну прямую, перпендикулярную другой плоскости, то такие

плоскости перпендикулярны. На рисунке 1.73 показаны взаимно перпендикулярные плоскости. На рисунке 1.74 показано построение плоскости, перпендикулярной заданной через точку А, используя условие перпендикулярности прямой (в данном случае главных линий) плоскости.

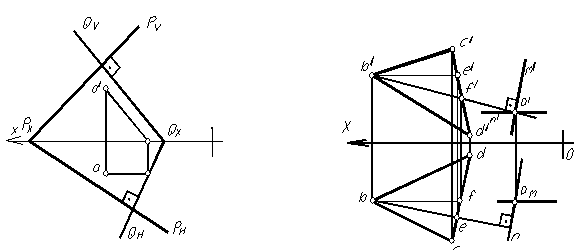В первом случае через точку А проведена фронталь, перпендикулярная плоскости Р, построен ее горизонтальный след и через него проведен горизонтальный след плоскости Q, перпендикулярно горизонтальному следу плоскости Р. Через полученную точку схода следов Q_X проведен фронтальный след плоскости Q перпендикулярно фронтальному следу плоскости Р.

Рис. 1.74

Во втором случае в плоскости треугольника проведены горизонталь ВЕ и фронталь BF и через заданную точку А задаем плоскость пересекающимися прямыми (главными линиями), перпендикулярную плоскости треугольника. Для этого проводим через точку А горизонталь и фронталь. Горизонтальную проекцию горизонтали искомой плоскости (N) проводим перпендикулярно горизонтальной проекции горизонтали треугольника, фронтальную проекцию фронтали новой плоскости (M) – перпендикулярно фронтальной проекции фронтали треугольника.

Дата добавления: 2014-01-06