З вивчення курсу

Сечение многогранников плоскостью. В сечении гранных поверхностей плоскостями получаются многоугольники, вершины которых определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью.

Рис. 1.80

Многоугольник сечения может быть найден двумя путями:

- вершины многоугольника находятся как точки пересечения прямых (ребер) с секущей плоскостью;

- стороны многоугольника находятся как линии пересечения плоскостей (граней) многогранника с секущей плоскостью.

В качестве примера построим сечение призмы фронтально-проецирующей плоскостью Q (рис. 1.80).

Секущая плоскость перпендикулярно фронтальной плоскости проекций, следовательно, все линии, лежащие в этой плоскости, в том числе и фигура сечения на фронтальной проекции, совпадут с фронтальным следом Qv плоскости Q. Таким образом, фронтальная проекция фигуры сечения 1/2/3/

Определяется при пересечении фронтальных проекций ребер призмы со следом Qv. Горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы. Профильная проекция фигуры сечения находится по принадлежностям проекций точек 1,2,3 соответствующим ребрам призмы. Если считать что плоскость Q отсекает верх призмы, то фигура сечения на профильной плоскости видна, а если нет, то линия 2//3// изобразится невидимой.

На рисунке 1.81 показано сечение четырехугольной пирамиды фронтально-проецирующей плоскостью Q.

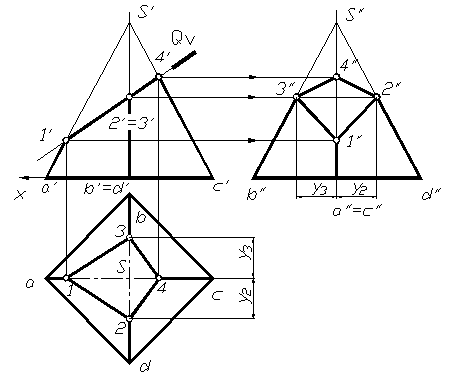
Рис. 1.81

Секущая плоскость перпендикулярна фронтальной плоскости проекций, следовательно, все линии, лежащие в этой плоскости, в том числе и фигура сечения на фронтальной проекции, совпадут с фронтальным следом плоскости. Таким образом, фронтальная проекция фигуры сечения 1,2,3,4 определится при пересечении фронтальных проекций ребер пирамиды со следом плоскости. Горизонтальные проекции этих точек находим, проводя проекционные линии связи на горизонтальную проекцию соответствующих ребер. Если считать что плоскость Q отсекает верх пирамиды, то на фронтальной плоскости фигура сечения видна, если нет, то 3//4//, 4//2//будут невидимы.

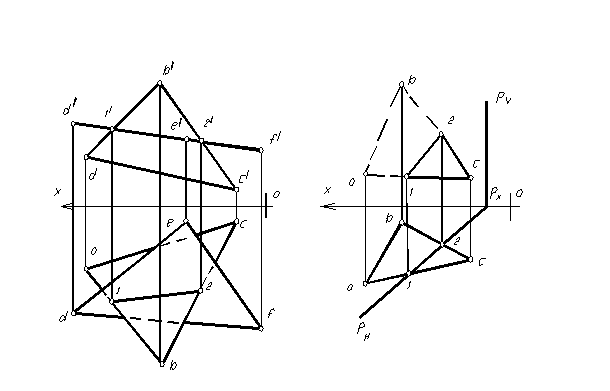
Призма с вырезом. В качестве примера построения сечения многогранника несколькими плоскостями рассмотрим построение призмы с вырезом, образованным треугольной призмой.

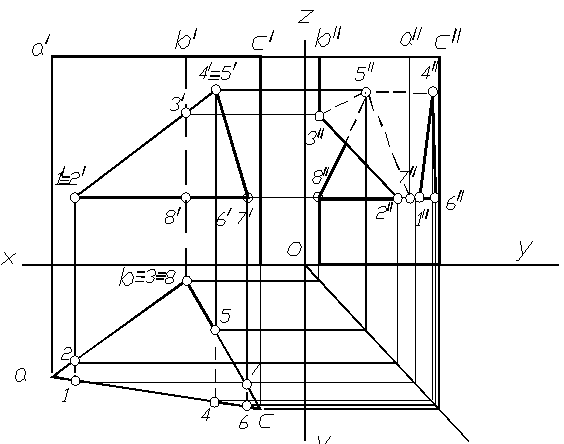Рис. 1.82

На фронтальной проекции отмечаем проекции точек встречи ребра B заданной призмы с гранями призмы выреза: 3/и 8/, и точки пересечения ребер призмы выреза с гранями заданного тела: 1/2/4/5/6/7/. Находим горизонтальные проекции отмеченных точек. Все они находятся на горизонтальной проекции заданной призмы. По двум полученным проекциям точек находим их профильные проекции. С учетом видимости соединяем точки, принадлежащие соответствующим граням заданной призмы. В грани AB: точки 3,2,8, в грани BC: точки 3,5,7,8 и в грани AC: 1,4,6,1.

Пирамида с вырезом. На рисунке 1.83 показано построение пирамиды с вырезом (как результат сечения пирамиды несколькими проецирующими плоскостями, образовавшими призматический вырез). Обозначаем на фронтальной проекции точки, одновременно принадлежащие заданной пирамиде и призматическому вырезу. По принадлежности точек ребрам заданной пирамиды находим их горизонтальные и профильные проекции. Точки (3) пересечения ребра призматического выреза с гранями заданной пирамиды можно найти двумя способами. Первый способ заключается в проведении через точки выреза плоскости S параллельной основанию (след которой обозначается на комплексном чертеже). В сечении пирамиды этой плоскостью образуется треугольник подобный основанию, проходящий через точку K. Данному треугольнику принадлежат точки 3,1,6,7,5,4,3. Можно также найти точки на поверхности пирамиды проведением через них прямых, связывающих их с вершиной пирамиды и дальнейшим построением проведенных прямых на горизонтальной плоскости проекций и нахождением на них искомых точек. Полученные точки соединяют с учетом видимости в необходимой последовательности по соответствующим граням заданной пирамиды (чтобы две точки принадлежали одной секущей плоскости и одной грани пирамиды).

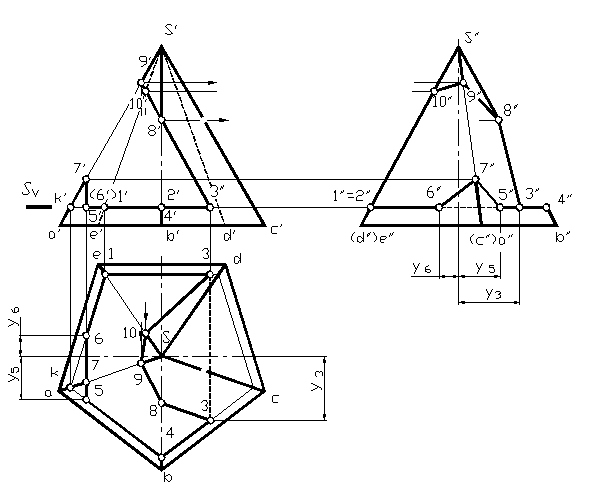
Рис. 1.83

1.18 Тела вращения

Рассмотрим некоторые из многочисленных поверхностей вращения.

Поверхности, образованные вращением прямой линии. К таковым относятся цилиндр и конус.

Цилиндр вращения – поверхность, полученная вращением прямой вокруг параллельной ей оси и ограниченная двумя взаимно параллельными плоскостями.

Конус вращения – поверхность, образованная вращением прямой (образующая) вокруг пересекающейся с ней осью (направляющая).

Примером поверхностей, образованных вращением окружности вокруг неподвижной оси является сфера.

Сфера – поверхность, полученная вращением окружности вокруг ее диаметра.

Сечение цилиндра плоскостью. При сечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получается пара прямых (образующих). Если секущая плоскость перпендикулярна к оси вращения, в сечении получается окружность. В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс.

Рис. 1.84

На рисунке 1.84 показан пример построения проекций линии сечения цилиндра фронтально проецирующей плоскостью Q, когда в сечении получается эллипс.

Фронтальная проекция фигуры сечения в этом случае совпадает с фронтальным следом плоскости, а горизонтальная – с горизонтальной проекцией поверхности цилиндра – окружностью. Профильная проекция строится по двум имеющимся проекциям – горизонтальной и фронтальной, замеряя игрековые координаты точек относительно оси цилиндра и откладывая их на проекционных линиях связи соответствующих точек.

Сечение конуса плоскостью. В зависимости от положения секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые линиями конических сечений.

Если секущая плоскость проходит через вершину конуса перпендикулярно его основанию, то в сечении получается пара прямых – образующих (треугольник – рис. 1.85а). В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность (рис. 185б). Если секущая плоскость наклонена к оси вращения конуса и не проходит через ее вершину, в сечении конуса могут получиться эллипс (секущая плоскость пересекает все образующие конуса – рис. 1.85в). Парабола образуется, если секущая плоскость параллельна одной из образующих конуса (рис. 1.85г). Гипербола образуется в случае, если секущая плоскость параллельна двум образующим конуса в зависимости от угла наклона секущей плоскости к основанию конуса (рис. 1.85д).

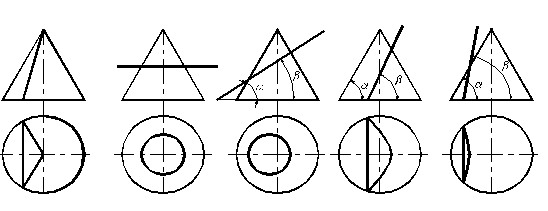
а б в г д

Рис. 1.85

Известно, что точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности. Для конуса графически наиболее простыми линиями являются образующие и окружности. Следовательно, если по условию задачи требуется найти горизонтальные проекции точек, принадлежащих поверхности конуса, то нужно через точки провести одну из этих линий.

На рисунке 1.86 дан пример построения проекций линии сечения конуса фронтально проецирующей плоскостью, когда в сечении получается эллипс.

Фигура сечения на фронтально плоскости совпадает со следом секущей плоскости. Обозначим характерные точки (точки, принадлежащие фронтальному очерку конуса – 1, 6 и 4, 5 – точки, принадлежащие профильному очерку конуса) и несколько промежуточных (чем больше будет отмечено таких точек, тем точнее получится фигура сечения – эллипс). Горизонтальные и профильные проекции точек 1,4,5,6, находятся без дополнительных построений, так как они принадлежат соответствующим очеркам конуса. Для точек 4 и 5 находятся их профильные проекции из условия принадлежности их профильному очерку конуса, а затем, измерив игрековую координату этих точек от оси конуса, отмечаются их горизонтальные проекции. Для нахождения проекций промежуточных точек можно воспользоваться методом проведения секущих плоскостей, параллельных основанию конуса или проведением через отмеченные точки образующих конуса с последующим нахождением горизонтальных проекций этих образующих и нахождением на них соответствующих точек. Далее по двум полученным проекциям строятся третью проекции отмеченных точек. Полученные проекции точек соединяются плавной кривой с учетом видимости (на примере верхняя часть конуса отсечена плоскостью Q и поэтому вся фигура сечения на профильной плоскости видна). Если такого отсечения не происходит, то на профильной проекции часть кривой сечения 465 изобразится невидимой линией.

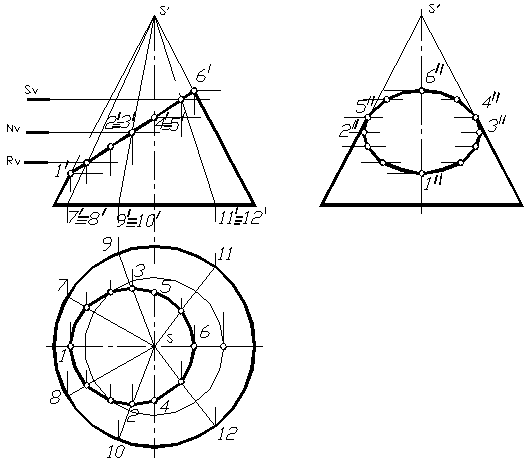
Рис. 1.86

Конус с вырезом. На рисунке 1.87 показан конус, в котором выполнен вырез, образованный тремя плоскостями частного положения, образующих призматический вырез. Фронтальная проекция фигуры сечения совпадает с очерком призматического выреза. Для нахождения горизонтально и профильной проекций выреза отмечаем ряд необходимых точек. Необходимо отметить характерные точки, принадлежащие очеркам конуса, точки перегиба плоскостей выреза и ряд промежуточных для точности построения определенных кривых.

В данном случае отмечаются точки 5,6 и 11,12, принадлежащие профильному очерку конуса; точки 1, 2, 3, 4, 9,10, являющиеся ребрами (линии перегиба плоскостей выреза) призматического выреза. Для более точного построения части параболы необходимо отметить ряд точек (чем их будет больше, тем точнее получится кривая) находящихся между точками 3, 9 и 4, 10 (в данном случае это точки 7 и 8). Для построения части выреза, в результате которого образуется часть гиперболы, отмечаются точки, находящиеся между точками 1 и 3, 2 и 4 (в данном случае это точки 13 и 14). Их также необходимо взять достаточное количество.

Построив горизонтальные и профильные проекции отмеченных точек, фигуры проекций выреза соединяются с учетом видимости. На горизонтальной плоскости линии входа и выхода призматического выреза конуса видны. На профильной проекции видимость определяется по граничным точкам 5, 6 и 11, 12. Линия 5, 7, 9, 11 и 6, 8, 10, 12 на профильной проекции не видна, но, учитывая форму выреза, куски линии 5, 7 и 6, 8 до линий 3, 13 и 4, 14 будут видны.

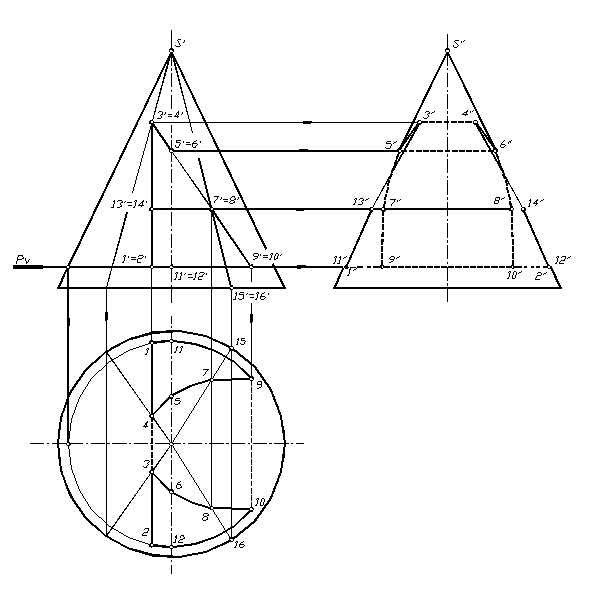
Рис. 1.87

Сечение шара плоскостью. Если шар пересекать плоскостью, то в сечении всегда получается окружность. Эта окружность может проецироваться:

- в прямую, если секущая плоскость перпендикулярна к плоскости проекций;

- в окружность с радиусом, равным расстоянию от оси вращения шара до очерка, если секущая плоскость параллельна какой-либо плоскости проекций;

- в эллипс, если секущая плоскость не параллельна ни одной из плоскостей проекций.

Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную какой-либо плоскости проекций, и построить окружность, на которой находится эта точка

На рисунке 1.88 показано построение проекций линии сечения шара фронтально проецирующей плоскость.

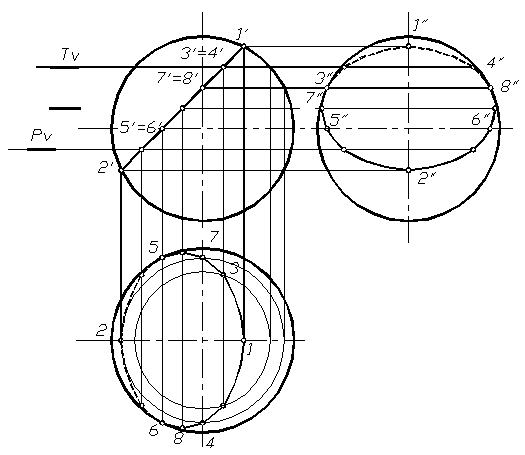
Рис. 1.88

Построение начинаем с определения характерных точек. Точки 1 и 2 находятся на фронтальном очерке шара (главном меридиане). Эти точки – концы малой оси эллипса, а также самая высокая и самая низкая точки. Их горизонтальные и профильные проекции находятся на соответствующих окружностях шара, которые на горизонтальной и профильной плоскостях совпадают с осями. Точки 7 и 8 находятся на профильном очерке шара (профильном меридиане) и служат для определения видимости на профильной плоскости проекций. Горизонтальные проекции этих точек находятся по фронтальным и профильным. Точки 5 и 6 находятся на горизонтальном очерке шара (экваторе) и служат для определения видимости на горизонтальной плоскости проекций. Профильные проекции этих точек находим по горизонтальным и фронтальным проекциям. Для точного построения линии сечения необходимо найти несколько дополнительных точек. Для их построения используются вспомогательные секущие плоскости (например, плоскости горизонтального уровня T и P), которые в сечении дают окружность на горизонтальной плоскости. Полученные точки соединяют плавной кривой с учетом их видимости.

Шар с вырезом. На рисунке 1.89 показано построение проекций шара с вырезом, образованным тремя плоскостями частного положения, образующими призматический вырез.

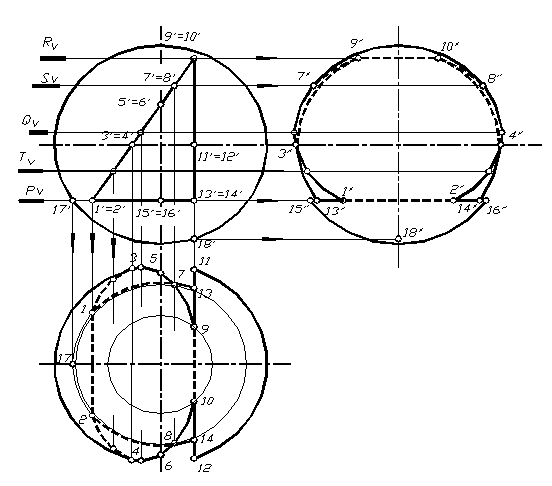
Рис. 1.89

Для построения проекций выреза отмечаем необходимые точки. Это точки, принадлежащие очеркам шара, точки перегиба плоскостей выреза, а также ряд промежуточных для более точного построения линий выреза.

Нахождение проекций характерных точек, принадлежащие очеркам шара, выполняется без дополнительных построений из учета принадлежности их определенным очеркам шара (точки 3, 4 и 11, 12 находятся на горизонтальном очерке шара, точки 7, 8 и 15, 16 – на профильном очерке). Проекции всех остальных точек находятся путем проведения через них дополнительных плоскостей уровня (горизонтального – как на данном примере или профильного). Например, при сечении шара плоскостью горизонтального уровня Р в сечении образуется окружность соответствующего радиуса. Горизонтальные проекции точек 1,2,15,16,13,14 находятся на горизонтальной проекции полученной окружности. Профильные проекции этих точек находятся по двум уже построенным фронтальным и горизонтальным. Кусочки линии сечения от этой плоскости с одной стороны шара: 1,15,13 и с другой – 2,16,14. Куски линии сечения шара в пределах выреза от плоскости, находящееся меду точками 1, 9 и 2, 10 с одной стороны шара: 1,3,5,7,9 и с другой – 2,4,6,8,10. Между точками 9, 13 и 10, 14 образуется часть окружности соответствующего радиуса, которая на горизонтальную плоскость проецируется в линию, а на профильную в окружность.

Полученные части линий проекций выреза соединяем с учетом видимости на горизонтальной и профильных плоскостях. Границей видимости на горизонтальной плоскости служат точки 3, 4 и 11, 12: на профильной плоскости – точки 5, 6 и 15, 16.

Литература

1. Бубенников А.В., Громов М.Я. Начертательная геометрия. М.: Высшая школа, 1973. – 243с., ил.

2. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии: Учеб. Пособие/Под ред. Ю.Б. Иванова. – 23 изд., перераб.–М.: Наука. Гл. ред. физ. мат. лит., 1988. – 272 с., ил.

3. Фролов С.А. Начертательная геометрия: Учеб. для вузов. – 2-е изд.,перераб. и доп. - М.: Машиностроение, 1983. – 240 с., ил.

4. Чекмарев А.А. Инженерная графика: Учеб. для машиностроит. спец. вузов. – 2-е изд., испр. – М.: Высш. Шк., 1998. – 365 с., ил.

«Основи екології»

Для студентів неекологічних спеціальностей

Миколаїв 2006 р.

Методичні рекомендації розроблені відповідно до навчальних планів факультетів університету на підставі нормативної для всіх неекологічних спеціальностей вищих закладів освіти програми курсу «Основи екології»,схваленої Міністерством освіти і науки України.

Методичні рекомендації призначені сприяти підвищенню якості підготовки студентів з основ екології.

Методичні рекомендації розроблені доцентом кафедри біології, кандидатом медичних наук Руденком Анатолієм Олександровичем.

Рецензенти:

Кісельов А.Ф. – кандидат медичних наук, професор

(МДУ ім.. В.О.Сухомлинського).

Роман І.І. – кандидат біологічних наук, доцент (Миколаївський державний аграрний університет).

Методичні рекомендації схвалені кафедрою біології.

Протокол засідання кафедри №8 від 21 березня 2006 р.

Методичні рекомендації рекомендовані до друку вченою радою Миколаївського державного університету

імені В.О.Сухомлинського (Протокол №10 від 29.05.2006 р.)

Дата добавления: 2014-01-06