Основные показатели динамики экономических явлений

При анализе временных рядов для определения изменений, происходящих в данном явлении, вычисляют следующие статистические показатели: абсолютные приросты, коэффициенты и темпы роста и прироста. Причем все эти показатели могут быть либо базисными, либо цепными. В основе расчета показателей динамики лежит сравнение уровней временного ряда. Если сравнение осуществляется с одним и тем же показателем, принятым за базу сравнения, то показатели называются базисными. Если каждый уровень сравнивается с предыдущим, то вычисленные показатели называются цепными.

Показателем скорости изучаемого явления служит абсолютный прирост, вычисляемый как разность двух уровней.

Базисные абсолютные приросты вычисляются по формуле

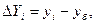
где y_i — i-й уровень временного ряда, i = 2, 3,…, n;

y_б — уровень, принятый за базу сравнения. Цепные абсолютные приросты вычисляются по формуле

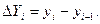
Для определения относительной скорости изучаемого явления в единицу времени используют относительные показатели — коэффициенты роста и.прироста.

Базисные и цепные коэффициенты роста вычисляют соответственно по формулам

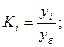
Тогда коэффициенты прироста равны: K_пр = K_i-1.

В качестве базисного уровня может быть выбран любой уровень в зависимости от целей исследования (обычно за базисный уровень выбирают первый уровень ряда у₁).

На практике чаще всего применяют показатели темпов роста и прироста (коэффициенты роста и прироста, выраженные в процентах):

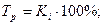
где T_p, — темп роста для i-го периода;

Т_пр — темп прироста для i-го периода.

Темп прироста показывает, на сколько процентов уровень одного периода увеличился (уменьшился) по сравнению с уровнем другого периода, т. е. он выражает относительную величину прироста в процентах.

Для получения обобщающих показателей динамики развития определяются средние величины: средний уровень ряда, средний абсолютный прирост, средние темпы роста и прироста.

Средний уровень ряда показывает, какая средняя величина уровня характерна для всего анализируемого периода. К расчету среднего уровня чаще всего прибегают для рядов, изменение которых относительно стабилизируется в течение большого периода времени (средний уровень урожайности за ряд лет), и рядов с колеблющимися уровнями за короткие промежутки времени (например, численность работников предприятий изменяется каждый день, и поэтому для отражения их работы рассчитывается показатель средней численности работников).

Средний уровень интервального ряда с равностоящими уровнями определяется по формуле

(1.1)

где n — длина временного ряда.

Средний уровень моментного ряда с равностоящими уровнями определяется по формуле

(1.2)

Величина среднего абсолютного прироста показывает скорость развития явления за изучаемый интервал времени и вычисляется по формуле

(1.3)

Для определения средней скорости изменения явления за рассматриваемый период времени берут средний темп роста. Чаще всего этот показатель рассчитывают по формуле средней геометрической:

(1.4)

Средний темп прироста соответственно равен:

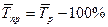
Показатель среднего темпа роста, рассчитываемый по формуле средней геометрической, основан на сопоставлении конечного и начального уровней временного ряда, а промежуточные уровни во внимание не принимаются. Поэтому для практических расчетов показатель, рассчитанный по формуле (1.4), можно использовать в случае более или менее равномерного изменения явления. В случае сильной колеблемости уровней за изучаемый промежуток времени применение этого показателя приведет к серьезным просчетам. В таком случае можно рассчитать средний темп роста по следующей формуле:

(1.5)

где 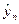, 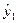— выравненные по уравнению тренда конечный и начальный уровни ряда.

Так как при расчете 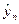и 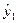учитывается колеблемость промежуточных уровней, то средний темп роста, вычисленный по формуле (1.5), будет более точно характеризовать явление за изучаемый период [24].

1.3. КОМПОНЕНТНЫЙ СОСТАВ ВРЕМЕННОГО РЯДА

Одной из основных задач анализа временных рядов является попытка выявить компоненты, на которые можно разложить уровни ряда динамики. Это разложение осуществляется на основе выделения факторов, под воздействием которых формируются показатели изучаемого явления. Принято выделять 4 типа таких факторов:

1) долговременные, формирующие общее направление развития (тенденцию) в изменении анализируемого явления. Обычно эта тенденция описывается с помощью той или иной монотонной неслучайной функции F_t, которая называется функцией тренда или просто трендом;

2) сезонные, формирующие периодически повторяющиеся в определенное время года колебания анализируемого явления. Эти колебания обычно описываются с помощью периодических функций;

3) циклические, формирующие изменения изучаемого явления, обусловленные действием долговременных циклов. Циклические изменения похожи на сезонные тем, что они являются повторяющимися и волнообразными, но отличаются большей длительностью циклов. Циклические колебания в экономических процессах примерно соответствуют циклам конъюнктуры;

4) нерегулярные, не поддающиеся учету и регистрации и делящиеся на 2 группы:

а) внезапные, приводящие к скачкообразным структурным изменениям в изучаемом процессе (например, война, эпидемия, экологические катастрофы и т. д.). Как правило, период, в который

возникают эти изменения, исключается из многолетних наблюдений;

б) случайные факторы, являющиеся результатом действия большого количества относительно слабых второстепенных факторов.

В процессе формирования временного ряда вовсе не обязательно участие факторов всех четырех типов, однако во всех случаях предполагается непременное участие случайных факторов.

В зависимости от того, как взаимосвязаны факторы между собой, можно построить следующие структурные схемы формирования значений Y_t:

Y_t = F_t + S_t + K_t + E_t — аддитивная схема; (1.6)

Y_t = F_tS_tK_tE_t — мультипликативная схема; (1.7)

Y_t = F_tS_tK_t + E_t — смешанная схема, (1.8)

где Y_t — уровни временного ряда;

F_t — трендовая компонента;

S_t — сезонная компонента;

K_t — циклическая компонента;

E_t — случайная компонента.

В экономических временных рядах предпочтение обычно отдается аддитивному представлению уровня ряда (1.6), в соответствии с которым временные ряды можно разделить на четыре группы.

К первой группе можно отнести временные ряды с тенденцией развития, но без периодической составляющей. Они, как правило, достаточно хорошо описываются аддитивной моделью

Y_t = F_t + E_t,

где F_t — некоторая неслучайная функция времени;

E_t — случайная составляющая.

Примером такого временного ряда могут быть данные об общем объеме розничного товарооборота в регионе по месяцам 1999 г. (рис. 1.1):

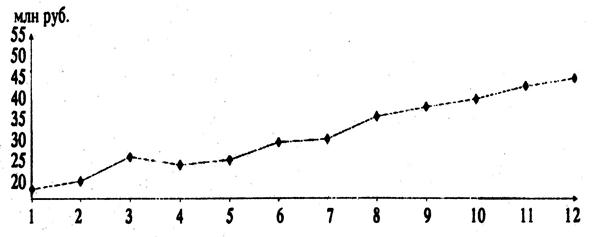
Рис. 1.1. Объем розничного товарооборота в регионе в 1999 г.

Ко второй группе относят временные ряды, имеющие в своем развитии сезонные колебания, наслаивающиеся на тренд. Их можно описать следующей аддитивной моделью:

Y_t = F_t + S_t + E_t,

где S_t — сезонная составляющая.

Примером может быть ряд, характеризующий динамику продажи молочных продуктов по кварталам за 4 года (рис. 1.2).

Рис. 1.2. Объем продажи молочных продуктов за 1996 — 1999 гг.

К третьей группе можно отнести временные ряды, не содержащие тенденции развития и периодические составляющие:

Y_t = E_t,

в которых значения y_t колеблются около некоторого постоянного уровня и носят случайный характер (например, ряд, отображающий динамику урожайности ячменя в Англии и Уэльсе за 20 лет (рис. 1.3.)).

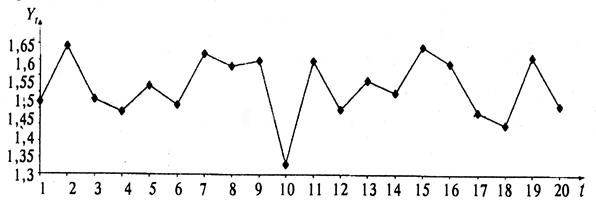
Рис. 1.3. Урожайность ячменя в Англии и Уэльсе с 1884 по 1904 г.

К четвертой группе относят временные ряды, включающие всевозможные виды колебаний (и сезонные, и циклические). Их структура не может быть однозначно описана с помощью известных функций, так как для разных участков ряда набор этих функций будет различным.

1.4. НЕКОТОРЫЕ ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

С точки зрения теории случайных процессов изменения, характеризующие реальные экономические процессы, описываются случайными функциями, значения которых в любой момент времени являются случайными величинами.

Случайные функции одной независимой переменной, за которую принимают время, называют случайными процессами.

Последовательность наблюдений Y(t₁), Y(t₂), …, Y(t_n) некоторого экономического процесса 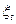называют реализацией случайного процесса. Последовательность наблюдений {Y(t_i)}, полученных в равностоящие моменты времени, называют временным или динамическим рядом [21].

С каждым случайным процессом 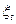обычно связывают несколько неслучайных функций: математическое ожидание, дисперсию, автокорреляционную и взаимную корреляционную функции.

Математическим ожиданием случайного процесса называют неслучайную функцию времени М[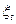], значения которой при t = t_i равны математическому ожиданию случайной величины 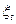. Это значит, что математическое ожидание случайного процесса есть некоторая средняя функция, вокруг которой варьируются результаты наблюдений.

Степень рассеивания этих наблюдений вокруг среднего значения характеризуется дисперсией случайного процесса.

Дисперсией случайного процесса 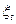называется неслучайная функция времени D [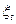], значения которой для каждого момента времени t = t_i равны дисперсии соответствующих случайных величин.

Таким образом, при рассмотрении математического ожидания и дисперсии случайного процесса видно, что процесс 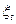разбивается на некоторую систематическую составляющую (среднюю) и отклонения от нее. При анализе временных рядов это находит свое отражение в представлении ряда Y_t в виде суммы

Y_t = F_t + Е„

где F_t — неслучайная функция времени, характеризующая систематическую составляющую;

Е_t — случайная компонента с нулевым математическим ожиданием и дисперсией D [].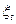

Для полной характеристики случайного процесса применяется автокорреляционная функция 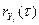, которая представляет собой множество коэффициентов корреляции между временным рядом Y_t и этим же рядом, сдвинутым во времени на величину τ. Нормированная автокорреляционная функция вычисляется по формуле

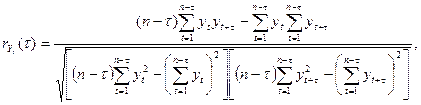(1.9)

где τ = 0, 1, 2, …, n-2; t = 1, 2, …, n-τ.

Автокорреляционная функция (1.9) называется нормированной, так как =1. Величину τ называют сдвигом. Сдвиг, которому соответствует наибольший коэффициент автокорреляции, называют временным лагом. График нормированной автокорреляционной функции называют коррелограммом. Он показывает, как часто и с каким запаздыванием изменение показателя y_t сказывается на последующих значениях этого показателя, при этом значения автокорреляционной функции могут колебаться от -1 до 1.

Автокорреляционная функция для случайной составляющей E_t имеет следующий вид:

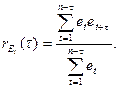(1.10)

Для одновременного сравнения и анализа двух случайных процессов по их заданным реализациям {Y_t} и {Х_t} используют взаимную корреляционную функцию. Нормированная взаимная корреляционная функция вычисляется по формуле.

(1.11)

Соответственно при вычислении взаимной корреляционной функции между случайными компонентами E_t и Z_t эта формула примет следующий вид:

(1.12)

Применение методов теории случайных процессов для анализа экономических временных рядов в значительной степени связано с проблемой исследования случайной составляющей E(t) и сравнения ее с другими случайными величинами, обладающими изученными свойствами. Это объясняется тем, что при краткосрочном и среднесрочном прогнозировании результаты прогнозов тесно связаны со случайной компонентой, в то время как при долгосрочном прогнозировании основное значение имеет определение тенденций и взаимосвязей между факторами.

В настоящее время наиболее изученными являются стационарные случайные процессы, которые протекают во времени приблизительно однородно и имеют вид непрерывных случайных колебаний вокруг некоторого среднего уровня, причем ни характер этих колебаний, ни средняя амплитуда со временем существенно не изменяются. Любой стационарный процесс можно рассматривать как процесс, продолжающийся во времени неопределенно долго. Поэтому при проведении исследований в качестве начала отсчета можно выбирать любой момент времени, причем на любом временном интервале должны быть получены одни и те же вероятностные характеристики. Поэтому стационарным процессом, в широком смысле слова, можно назвать такой случайный процесс, у которого математическое ожидание постоянно, а автокорреляционная функция не зависит от времени, и для этого процесса выполняются следующие соотношения:

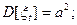
где τ = t_i - t_j.

Величина автокорреляционной функции не зависит от начала отсчета, а зависит только от величины сдвига τ. Значение 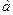определяет постоянный уровень, относительно которого варьируют значения временного ряда Y_t, а постоянная величина σ² характеризует размах этой вариации. Поскольку закон распределения вероятностей случайной величины 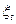одинаков для всех t, то основные характеристики стационарного случайного процесса могут быть оценены по наблюдениям y₁, y₂, …, y_n как

В экономической практике в большинстве случаев приходится иметь дело с процессами, имеющими вполне определенную тенденцию развития явления во времени. Такие процессы называются нестационарными. Характеристики нестационарных случайных процессов меняются во времени, т. е. зависят от начала отсчета. В ряде случаев эти процессы на определенных интервалах времени условно могут быть приняты за стационарные. Тогда на них могут быть перенесены все основные выводы стационарных случайных процессов. Те экономические процессы, которые содержат явно выраженную тенденцию, можно преобразовать в стационарные путем исключения тенденции и периодических колебаний из временных рядов, если таковые имеются.

Таким образом, исходя из вышеизложенного можно сформулировать основные задачи статистического анализа временного ряда.

По имеющимся значениям y₁, y₂, …, y_n анализируемого временного ряда требуется:

а) определить, какие из неслучайных функций F_t, К_t, S_t присутствуют в аддитивном разложении (1.6);

б) построить „хорошие" оценки для этих неслучайных функций и в первую очередь определить наилучшим образом оценку долговременной составляющей (тенденции), которая отражает основные закономерности изменения исследуемой характеристики во времени;

в) подобрать модель, адекватно описывающую поведение случайной компоненты Е_t, и статистически оценить ее параметры.

Успешное решение этих задач является основой для достижения конечных целей исследования, и в первую очередь для построения кратко- и среднесрочного прогнозов значений временного ряда.

Дата добавления: 2014-01-06