
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статистический анализ сезонной компоненты
|
|
|
|
ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ С ПОМОЩЬЮ АВТОРЕГРЕССИОННЫХ МОДЕЛЕЙ
Как было отмечено выше, при подтверждении случайности и стационарности ряда остатков для их описания можно применять модели авторегрессии. Если исследуемый ряд представляется в виде суммы долговременной составляющей (тренда) и случайной компоненты, то общий прогноз показателя может быть сделан по обеим составляющим ряда: по тренду — путем простой экстраполяции, по отклонениям — по модели авторегрессии. Сумма двух прогнозов даст общий суммарный прогноз для исследуемого ряда.
Применение авторегрессионных моделей для прогнозирования ряда остатков возможно лишь после проведения следующих этапов.
1. Из временного ряда следует выделить случайный компонент
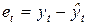 .
.
2. Провести проверку: является ли случайный компонент величиной, не зависящей от времени (см. п. 3.1).
3. Проверить гипотезу о стационарности случайного компонента (см. п. 3.4).
4. Построить модель авторегрессии для ряда остатков еt (см. п. 4.1 — 4.2).
5. Проверить гипотезу о нормальном распределении ряда отклонений от расчетных значений, полученных по авторегрессионной модели (см. п. 3.3).
6. Проверить независимость ряда отклонений от расчетных значений, полученных по авторегрессионной модели (см. п. 3.2).
Если при проверке установлено, что для временного ряда не выполняются условия 2-го и 3-го этапов, то для описания процесса неправомерно применять авторегрессионную модель. Если не выполняются условия 5-го и 6-го этапов, то рассматриваемый процесс Et следует описать авторегрессией более высокого порядка.
После того как произведены необходимые проверки и вычислены коэффициенты авторегрессии, можно найти прогнозные значения εt на период (t + 1) следующим образом.
Сначала вычисляют значение 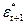 по формуле
по формуле
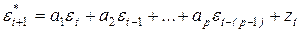 . (5.7)
. (5.7)
Затем в модель
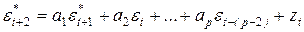 (5.8)
(5.8)
подставляют вычисленное значение 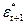 и определяют величину прогноза
и определяют величину прогноза 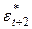 и т. д., где zt — остатки ряда Et, называемые „белым шумом".
и т. д., где zt — остатки ряда Et, называемые „белым шумом".
В том случае, если сам временной ряд Yt является стационарным случайным процессом, т. е. Еt = Yt, прогноз осуществляется по формулам (5.7), (5.8), где вместо значений εt берутся уровни yt. Вероятностные границы предсказанного значения yt можно получить с помощью следующего интервала:
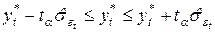 ,
,
где  — предсказывемое значение исследуемого параметра;
— предсказывемое значение исследуемого параметра;
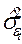 — оценка дисперсии случайной величины εt,
— оценка дисперсии случайной величины εt,
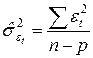 ,
,
где n — число наблюдений;
р — порядок авторегрессионной модели.
П р и м е р 5.4. В качестве примера построения авторегрессионных моделей при прогнозировании был взят временной ряд, рассмотренный в примере 2.3. Для представленного в табл. 2.5 временного ряда тренд был выбран в виде параболы
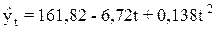 .
.
Для проверки, насколько удачно исключен тренд из временного ряда, применим критерий „восходящих" и „нисходящих" серий. Чтобы определить левые части неравенств (2.1), были подсчитаны протяженность самой длинной серии Kmax(n) = 4 и общее число серий ν(n) = 12. Затем были найдены правые части неравенств. Сравнение левых и правых частей неравенств позволило сделать вывод, что оба они справедливы. Таким образом, можно считать, что тренд исключен из временного ряда удачно, а отклонения от тренда носят случайный характер.
Далее проверялась гипотеза о том, что случайная компонента представляет собой стационарный случайный процесс (см. п. 3.4). Были подсчитаны значения автокорреляционной функции соответственно для 24, 23, 22, 21, 20, 19 и 18 наблюдений, причем из расчетов последовательно исключались первый, второй и т. д. уровни. Большее число наблюдений исключать нецелесообразно, так как ряд отклонений от параболического тренда слишком короткий. Для всех значений коэффициентов автокорреляции рассчитывались величины z-критерия Фишера. Затем для каждого сдвига τ определялись величины 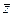 ,χ2. Все расчеты представлены в табл. 5.2.
,χ2. Все расчеты представлены в табл. 5.2.
Т а б л и ц а 5.2
Проверка стационарности отклонений от параболического тренда
| Число наблюдении | Сдвиги | ||||||||
| r и z | |||||||||
| r | 0,731 | 0,427 | 0,104 | -0,156 | -0,383 | -0,549 | - 0,565 | - 0,527 | |
| z | 0,931 | 0,456 | 0,104 | -0,157 | - 0,403 | -0,617 | - 0,640 | -0,586 | |
| r | 0,729 | 0,452 | 0,224 | -0,102 | -0,334 | - 0,496 | - 0,546 | - 0,529 | |
| z | 0,926 | 0,487 | 0,227 | -0,103 | - 0,347 | - 0,544 | -0,612 | - 0,589 | |
| r | 0,761 | 0,576 | 0,304 | - 0,028 | - 0,254 | - 0,457 | -0,530 | -0,513 | |
| z | 0,998 | 0,656 | 0,314 | - 0,028 | - 0,260 | -0,493 | -0,591 | - 0,566 | |
| r | 0,801 | 0,605 | 0,339 | 0,012 | -0,226 | -0,438 | -0,512 | -0,508 | |
| z | 1,100 | 0,701 | 0,352 | 0,012 | -0,229 | -0,470 | -0,565 | -0,561 | |
| r | 0,808 | 0,575 | 0,264 | - 0,066 | -0,307 | - 0,539 | - 0,584 | -0,494 | |
| z | 1,122 | 0,655 | 0,271 | - 0,066 | -0,317 | - 0,602 | -0,668 | - 0,542 | |
| r | 0,785 | 0,523 | 0,216 | -0,116 | -0,372 | - 0,589 | - 0,573 | - 0,462 | |
| z | 1,058 | 0,581 | 0,219 | -0,117 | - 0,391 | -0,676 | -0,653 | - 0,500 | |
| r | 0,740 | 0,480 | 0,163 | -0,206 | -0,450 | - 0,593 | - 0,552 | - 0,400 | |
| z | 0,951 | 0,523 | 0,164 | -0,209 | -0,485 | -0,682 | -0,622 | -0,424 | |
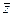
| 1,012 | 0,580 | 0,236 | -0,095 | -0,348 | - 0,584 | -0,621 | - 0,538 | |
| χ2 | 0,795 | 1,014 | 0,786 | 0,580 | 0,745 | 0,636 | 0,108 | 0,270 |
Верхняя граница для χ2 с 6 степенями свободы при 5-м уровне значимости равна 12,59. Из табл. 5.2 видно, что все вычисленные значения 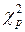 меньше этой величины. Следовательно, гипотеза об однородности коэффициентов автокорреляции для каждого сдвига может быть принята. Тем самым гипотезу о том, что отклонения от параболического тренда являются стационарным процессом, также можно принять.
меньше этой величины. Следовательно, гипотеза об однородности коэффициентов автокорреляции для каждого сдвига может быть принята. Тем самым гипотезу о том, что отклонения от параболического тренда являются стационарным процессом, также можно принять.
Первым шагом при выборе порядка авторегрессионой модели является анализ коррелограмма (рис. 5.1).
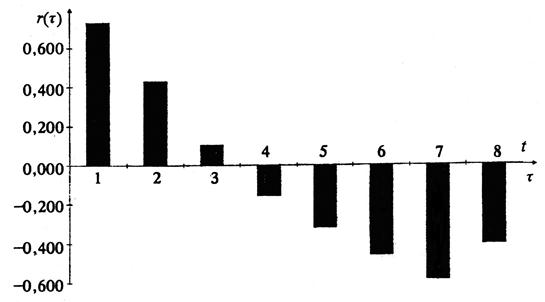
Рис. 5.1. График автокорреляционной функции
По графику автокорреляционной функции (см. рис. 5.1) видно, что она имеет затухающие синусоидальные колебания и достигает наибольшей величины на первом сдвиге (соответствующий коэфициент автокорреляции равен 0,731). Поэтому первоначально была построена авторегрессионная модель 1-го порядка
εt = 0,7358εt-1 + zt.
Далее по критерию Бартлетта проверяется гипотеза о том, что авторегрессионная модель 2-го порядка
εt = 0,9395εt-1 + 0,2168εt-2
не дает лучшей аппроксимации по сравнению с моделью 1-го порядка. Расчетное значение критерия Бартлетта составило 2,81. Табличное значение χ2 для 5% уровня значимости и 1-й степени свободы равно 3,84. Следовательно, гипотеза о том, что модель 2-го порядка не является лучшей по сравнению с моделью авторегрессии 1-го порядка, принимается. Проверим далее, существенна ли автокорреляция для остатков (zt = εt – εt - i) в модели 1-го порядка. Расчетное значение критерия d равно 1,52. Табличное значение d2 для 5% уровня значимости равно 1,45. Следовательно, гипотеза об отсутствии автокорреляции в отклонениях от модели 1-го порядка принимается.
Проверим теперь последнее условие — нормально ли распределена величина zt. Поскольку мы имеем небольшое число наблюдений для z, то такая проверка проводится на основании показателей асимметрии и эксцесса (см. п. 3.3). Для этого были подсчитаны выборочные показатели асимметрии эксцесса и их ошибки (3.2) — (3.5) и составлены неравенства (3.6). Проверка показала, что оба неравенства справедливы. Поэтому гипотеза о нормальном характере распределения величины zt не отвергается.
Таким образом, проверка основных предпосылок показала правильность гипотезы о том, что отклонения от тренда могут быть достаточно точно аппроксимированы авторегрессионной моделью 1-го порядка (5.9).
Из формулы разложения ряда на составляющие
yt = 161,820 - 6,720t + 0,138t2 + εt
случайная компонента может быть выражена как
εt = yt - 161,820 + 6,720t – 0,138t2 (5.10)
Подставив в выражение (5.10) вместо εt равенство (5.9), получим:
yt - 161,820 + 6,720t - 0,138t2 = 0,7258(yt-1 - 161,820 + 6,720(t-1) - 0,138(t-1)2)+ zt.
В результате соответствующих преобразований модель прогноза имеет вид
yt = 0,7358уt-1 - 1,9780t + 0,2400t2 + 37,9100 + zt
Используя полученную модель, построим прогноз исследуемого временного ряда на 4 дальнейших периода. Результаты представлены в табл. 5.3.
Т а б л и ц а 5.3
Прогноз продажи мяса на 2000 год
| Квартал | Прогноз | Нижняя граница прогноза | Верхняя граница прогноза |
| I | 82,59 | 72,98 | 96,98 |
| II | 82,28 | 69,14 | 98,95 |
| Ш | 82,42 | 67,46 | 99,97 |
| IV | 82,96 | 66,96 | 100,86 |
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 341; Нарушение авторских прав?; Мы поможем в написании вашей работы!