Допустимые базисные решения и многогранник решений

В задачах линейного программирования представляют интерес системы, в которых ранг r матрицы коэффициентов системы А = (а_ij), i = 1, 2,..., m; j= 1, 2,..., N, или, что то же самое, максимальное число независимых уравнений системы r меньше числа переменных, т.е. r < N. Будем полагать, что все m уравнений системы независимы, т.е. r=m и соответственно m < N.

Любые m переменных системы m линейных уравнений с N переменными (m < N) называются основными (или базисными ), если определитель матрицы коэффициентов при них отличен от нуля. Остальные (N-m) переменных называются неосновными (или свободными ). Основными могут быть разные группы из N переменных. Максимально возможное число групп основных переменных равно числу способов выбора т переменных из их общего числа N, т.е. числу сочетаний 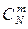. Но так как возможны случаи, когда определитель матрицы коэффициентов при т переменных равен нулю, то число групп основных переменных не превосходит .

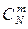Теорема. Если для системы m линейных уравнений с N переменными (где m < N) ранг матрицы коэффициентов при переменных равен m, т.е. существует хотя бы одна группа основных переменных, то эта система является неопределенной, причем каждому произвольному набору значений неосновных переменных соответствует одно решение системы.

Решение системы называется допустимым, если оно содержит лишь неотрицательные компоненты, т.е. х_j ³ 0 для любых j = 1, 2,..., N. В противном случае решение называется недопустимым.

Среди бесконечного множества решений системы выделяют так называемые базисные решения. Базисным решением системы m линейных уравнений с N переменными называется решение, в котором все (N - m) неосновных переменных равны нулю. В задачах линейного программирования особый интерес представляют допустимые базисные решения (опорные планы). Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным.

Множество допустимых решений системы ограничений задачи линейного программирования является выпуклым многогранником.

Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника ограничений, и наоборот, каждой угловой точке многогранника ограничений соответствует допустимое базисное решение.

Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника ограничений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Следовательно, оптимум линейной функции задачи линейного программирования следует искать среди конечного числа ее допустимых базисных решений.

Дата добавления: 2014-01-06