Определение первоначального допустимого базисного решения

При выборе первоначального базисного решения рекомендуется придерживаться следующего алгоритма:

1) Если каждая дополнительная переменная входит в уравнение с тем же знаком, что и свободный член, стоящий в правой части уравнения, то дополнительные переменные можно брать в качестве основных на первом шаге (см. Пример 2).

2) Если первое базисное решение получилось недопустимым (например, в качестве основных взяты дополнительные переменные и хотя бы одна из них входила в уравнение со знаком, противоположным знаку свободного члена), то следует рассмотреть уравнение, содержащее отрицательный свободный член и перевести в основные ту неосновную переменную, которая входит в это уравнение с положительным коэффициентом. Такие шаги повторяются до тех пор, пока не будет получено допустимое базисное решение (см. Пример 3).

3) Если базисное решение недопустимое, а в уравнении, содержащем отрицательный свободный член, отсутствует переменная с положительным коэффициентом, то в этом случае допустимое базисное решение получить нельзя из-за противоречивости условий задачи.

Пример 4. К условиям задачи из примера 1 добавим требование выпустить продукцию вида Р₁ в количестве не менее 5 единиц.

Построим математическую модель задачи.

Найти значения переменных х₁, х₂, удовлетворяющие условиям:

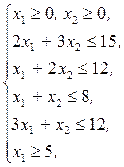(2.19)

при которых целевая функция 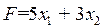принимает максимальное значение.

Приведем систему к каноническому виду введением дополнительных переменных: ,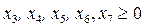

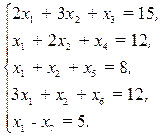(2.20)

В качестве базисных переменных выберем дополнительные переменные 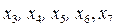. Из каждого уравнения выразим базисные переменные через неосновные:

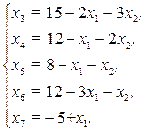(2.21)

Первоначальное базисное решение является недопустимым: 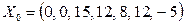. Можно перевести в базис переменную х₁. Выразив её из последнего уравнения, и подставляя в остальные уравнения и целевую функцию, получим:

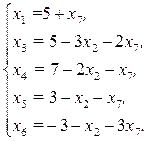(2.22)

Полученное базисное решение снова является недопустимым: 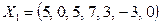. При этом в уравнении, содержащем отрицательный свободный член, отсутствует переменная с положительным коэффициентом. Т.е. в этом случае допустимое базисное решение получить нельзя из-за противоречивости условий задачи. Действительно, если вспомнить оценочные отношения, вычисленные нами на первом шаге при решении примера 1, то увеличивать переменную х₁ можно было только до 4.

Дата добавления: 2014-01-06