
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Судовые микропроцессорные системы управления
|
|
|
|
Задача управления производством и запасами
Задача о замене.
Задача оптимального распределения ресурсов.
Полученные рекуррентные соотношения называют функциональными уравнениями Беллмана.
При этом согласно определению zn(x0) = F*.
а) Постановка задачи.
Задачи на оптимальное распределение ресурса, который можно использовать различным образом, возникают при разработке оперативных и перспективных планов особенно часто. К ним относятся задачи о распределении средств на приобретение оборудования, закупку сырья и найм специалистов; задачи о распределении товара по торговым предприятиям и складам; задачи по определению последовательности пропорций между продукцией с/х производства, предназначенной для реализации и воспроизводства и т.д.
Рассмотрим задачу оптимального распределения заданного объема капиталовложений в несколько предприятий.
Пусть на реконструкцию и модернизацию 4-х своих филиалов фирма имеет возможность выделить 200 млн. руб. Ожидаемый прирост прибыли зависит как от финансируемого филиала, так и от объема этого финансирования. Однако, прирост прибыли в отдельно взятом филиале не зависит от вложенных средств в другие филиалы, а общая прибыль фирмы равна сумме всех приростов по филиалам. Следует определить оптимальное распределение капиталовложений между филиалами, максимизирующее общий прирост прибыли фирмы.
В данном случае речь идет об однократном распределении средств, и поэтому задача сама по себе не является динамической. Однако, ее можно наиболее просто решить как «многошаговую», если объекты капиталовложений (филиалы) включать в рассмотрение последовательно, т.е. на каждом шаге к рассмотренным добавлять следующий.
При таком подходе можно использовать функциональные уравнения Беллмана. Для их решения в табулированном виде общий объем капиталовложений разбивается на N интервалов с шагом 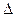 (для нашей задачи положим N = 4, тогда
(для нашей задачи положим N = 4, тогда 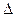 = 200/4=50 млн. руб.). Т.е. значения функций, входящих в уравнения Беллмана, будут определяться только в точках, кратных
= 200/4=50 млн. руб.). Т.е. значения функций, входящих в уравнения Беллмана, будут определяться только в точках, кратных 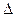 (в нашем примере в точках 0, 50, 100, 150, 200).
(в нашем примере в точках 0, 50, 100, 150, 200).
Пусть ожидаемый прирост прибыли филиалов при соответствующих капиталовложениях задан таблицей.
| Кап. Вложения | Прирост прибыли по филиалам | |||
С =200 – общий объем распределяемых средств;
х - объем средств, выделяемых филиалам (на каждом шаге), 0≤ х ≤C.
Fi(xi) – ожидаемый прирост i-той фирмы при выделении ей хi средств. Тогда целевая функция
F = F1(x1) + F2(x2) + F3(x3) + F4(x4) → max
при ограничении x1 + x2 + x3 + x4 = C, xi ≥ 0, i =  .
.
б) Схема решения.
1. Введем последовательность функций:
z1(x) – max прибыль фирмы, если x средств выделить одному 1-му филиалу;
z2(x) – max прибыль фирмы, если x средств распределить между 1-м и 2-м филиалами;
z3(x) – max прибыль фирмы, если х средств распределить между 3-м и двумя первыми
филиалами;
z4(x) – max прибыль фирмы, при распределении x средств между всеми 4-мя
филиалами.
Очевидно, что z4(C) = max F = F*, a zi(0) = 0.
2. «Обратный ход».
Рассмотрим финансирование только 1-го филиала, тогда по определению
z1(x) = F1(x). (1)
Пусть теперь средства в объеме x распределяются между 1-м и 2-м филиалами: 2-му в объеме x2, тогда х – х2 = х1 выделяется 1-му. Общая прибыль двух филиалов
z2(x) =  (F2(x2) + z1(x – x2)). (2)
(F2(x2) + z1(x – x2)). (2)
Теперь включим в рассмотрение дополнительно 3-й филиал: из общей суммы х выделим 3-му филиалу х3, тогда остальная часть х – х3 оптимальным образом распределяется между двумя первыми
z3(x) = 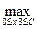 (F3(x3) + z2(x – x3)). (3)
(F3(x3) + z2(x – x3)). (3)
Наконец, по аналогии находим
z4(x) =  (F4(x4) + z3(x – x4)). (4)
(F4(x4) + z3(x – x4)). (4)
3. «Прямой ход».
Функциональные уравнения Беллмана (1) – (4) позволяют рассчитать значения zi и Fi для всех возможных х. Среди них находим z4(C) = F* и оптимальное x4* такое, что
F4(x4*) = F4*, после чего результаты вычислений просматриваются в обратном порядке. Зная x4*, находим С–х4* - объем финансирования остальных трех филиалов, а следовательно, и F3* и х3*, и т.д. до нахождения х1* и F1* = F1(x1*).
в) Расчет.
….
а) Постановка задачи.
Оборудование со временем изнашивается и стареет морально, падает его производительность, растут издержки на ремонт. Поэтому на каком-то этапе его эксплуатация становится менее выгодной, чем замена на новое. Возникает задача определения оптимальной стратегии замены оборудования в рассматриваемый временной промежуток – плановый период (п/п) с тем, чтобы суммарная прибыль за этот период была оптимальной.
Введем обозначения.
r(t) – стоимость продукции, производимой за год на оборудовании возраста t;
s(t) – остаточная стоимость оборудования возраста t;
u(t) – эксплуатационные издержки за год оборудования возраста t;
p – цена нового оборудования, которым можно заменить устаревшее:
n – число лет в рассматриваемом п/п.
Для дискретности решения задачи возраст оборудования t будем отсчитывать с интервалом 1 год. Управление составляют два возможных решения на каждом этапе (в начале каждого года): «сохранение» – продолжение эксплуатации имеющегося оборудования; «замена» – реализация старого оборудования по остаточной стоимости и приобретение нового по цене p. Целевая функция – суммарная прибыль за п/п F→max. Ограничения определяются критерием замены оборудования: прибыль при дальнейшей эксплуатации старого меньше прибыли после его замены с учетом всех издержек. Если прибыль от нового оборудования равна прибыли при старом, то старое сохраняется еще на год, т.к. оно уже досконально изучено.
б) Схема решения.
Задача решается методом ДП на основе принципа оптимальности Беллмана. В процессе «обратного хода» рассматриваются этапы – временные шаги от конца п/п к его началу.
Введем последовательность функций: zi(t), i =  – максимальная прибыль за последние i лет п/п. Очевидно, что zn(t0) = max F = F*, где t0 – возраст оборудования в начале п/п. Итак, сначала рассматриваем только последний n-ый год п/п, i = 1. Пусть в начале этого года, когда оборудование имеет возраст t лет, выбирается одно из управлений: 1) сохранение оборудования на n-ый год, тогда прибыль за оставшийся год п/п составит r(t) – u(t); 2) замена новым, продажа старого по остаточной стоимости, тогда прибыль составит s(t) – p + r(0) – u(0), где r(0) – стоимость продукции, на новом оборудовании за 1-й год его эксплуатации, u(0) – эксплуатационные издержки нового оборудования за 1-й год. Определяем оптимальное управление, исходя из критерия замены:
– максимальная прибыль за последние i лет п/п. Очевидно, что zn(t0) = max F = F*, где t0 – возраст оборудования в начале п/п. Итак, сначала рассматриваем только последний n-ый год п/п, i = 1. Пусть в начале этого года, когда оборудование имеет возраст t лет, выбирается одно из управлений: 1) сохранение оборудования на n-ый год, тогда прибыль за оставшийся год п/п составит r(t) – u(t); 2) замена новым, продажа старого по остаточной стоимости, тогда прибыль составит s(t) – p + r(0) – u(0), где r(0) – стоимость продукции, на новом оборудовании за 1-й год его эксплуатации, u(0) – эксплуатационные издержки нового оборудования за 1-й год. Определяем оптимальное управление, исходя из критерия замены:
- если s(t) – p + r(0) – u(0) ≤ r(t) – u (t), то «сохранить»,
- если s(t) – p + r(0) – u(0) > r(t) – u(t), то «заменить».
z1(t) = max
Теперь включаем в рассмотрение предпоследний шаг, (n – 1)-й год, i = 2 и установим прибыль за два последних года z2 (t).
Пусть в начале (n – 1)-го года возраст оборудования t, и было принято решение о его сохранении. Тогда прибыль к концу года зависит r (t) – u (t). При этом на начало n-го года оборудование уже будет иметь возраст t+1, следовательно, в последнем году оно даст прибыль z1(t+1), а общая прибыль за два последних года составит r (t) – u (t) + z1(t+1).
Если же в начале (n-1)-го года выбрано управление ”замена”, то прибыль за два последних года составит s (t) – p + r (0) – u (0) + z1(1), следовательно,
z2(t) = max
Аналогично для i последних лет:
zi(t) = max 
Дойдя до последнего шага (i = n), попадаем в начало п/п, где t известно: t = t0, и, следовательно, можно начать ”прямой ход”.
Задавая t0 и длительность п/п, находим F* = zn(t0) и строим последовательность оптимальных управлений, начиная с первого года и заканчивая последним.
в) Расчет.
Для заполнения расчетной таблицы можно использовать следующий алгоритм.
1. Определить φ (t) = r(t) – u(t), m1 = S(t) – p + φ(0):
- если m1 = const, то справа к таблице прибавляется дополнительный столбец mi;
- если m1 = m1(t), то над каждой строкой zi(t) вводится дополнительная строка mi = mi(t)
(или mi(t) вписывается в клетки значений zi(t) как тарифы транспортной задачи).
2. Заполнить строку z1(t), переписав из таблицы данных соответствующие значения
φ(t) ≥ m1, все значения φ(t) < m1 заменить на m1.
3. Начиная с индекса i = 2, расчет по строкам производится в следующей последовательности:
а) вычислить mi = m1 + zi-1(1), где zi-1(1) берется из уже заполненной строки;
б) вычислить zi(t) = z1(t) + zi-1(t+1), где сумма и слагаемые образуют треугольник, у
которого одна из вершин всегда в первой строке над искомым значением, а 2-ая - в
последней заполненной строке следующего столбца. Получаемые значения zi(t) ≥ mi
вносить в соответствующие клетки строки; начиная с первого zi(t) < mi, оставшиеся
клетки заполнить значением mi;
в) клетки с первым значением zi(t) < mi в процессе заполнения таблицы отделить от
расположенных в строке левее разделительной границей смены управления;
г) если таблица не заполнена до последней строки, перейти к п. а) и выполнить расчет
для следующего значения индекса i.
Замечания:
1. Для задачи об оптимальном распределении капиталовложений по полученной расчетной таблице можно получить стратегию вложения средств, например, только в первые 3 филиала, исключив из рассмотрения 4-й, или, например, для суммы в 150 млн. руб. (а не 200) между 4-мя филиалами, или только 3-мя первыми и т.д.
Для задачи о замене по расчетной таблице можно получить решение на любой п/п длительностью, не превосходящей исходный.
Это так называемый «принцип погружения» метода динамического программирования.
2. Решенную задачу о замене оборудования можно усложнить, например, допуская замену не новым оборудованием, а уже проработавшим некоторое время. При этом имеется три возможных управления: сохранить старое, купить новое, купить не новое.
Предприятие производит партиями некоторые изделия. Оно получило заказы на n месяцев. Необходимо составить план производства на указанные n месяцев с учетом затрат на производство и хранение. Обозначим:
1) xj – число изделий, производимых в j-м месяце;
2) yj - величина запаса к началу j-го месяца (Это число не содержит изделий,
производимых в j-й месяц, величина запаса к началу 1-го месяца (y1) и к концу
последнего (yn+1) заданы);
3) dj – число изделий, которые должны быть отгружены в j-й месяц;
4)  - функция затрат на производство xj изделий в j-м месяце (может
- функция затрат на производство xj изделий в j-м месяце (может
иметь и другой вид);
5) hj – затраты на хранение единицы запаса, переходящей из месяца j в месяц (j+1);
6)  - функция затрат на производство и хранение в j-м месяце.
- функция затрат на производство и хранение в j-м месяце.
Задача состоит в определении плана производства (х1,х2,…,хn), компоненты которого удовлетворяют условиям материального баланса
xj +yj –dj = yj+1 
и минимизируют суммарные затраты за весь период
 .
.
По смыслу  ,
,  ,
, . Заметим, что:
. Заметим, что:
1) для любого месяца j величина запаса к концу месяца должна удовлетворять ограничениям
 ,
,
то есть объем производимой продукции xj в j-м месяце может быть настолько
велик, что запас yj+1 удовлетворяет спрос на всех последующих месяцах, но не
имеет смысла иметь yj+1 больше суммарного спроса всех последующих месяцев;
2) из балансового уравнения получим  .
.
Если учесть, что xj и yj должны быть целыми и неотрицательными, то имеем задачу целочисленного нелинейного программирования.
Составим функциональные уравнения. Пусть Fk(yk+1) - минимальные затраты за
первые k месяцев.
Для k = 1:


при 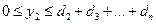 и
и  . На начальном этапе при фиксированном значении y1 исходного запаса каждому значению y2 отвечает только одно значение x1.
. На начальном этапе при фиксированном значении y1 исходного запаса каждому значению y2 отвечает только одно значение x1.
Для k  2:
2: 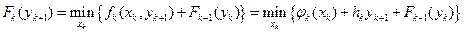
при  ,
, 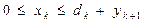 и
и  .
.
Применив процедуру динамического программирования, на последнем шаге k = n определяется значение xn* оптимального решения, а остальные компоненты определяются в результате прямого хода по формуле

 .
.
оглавление
Лекция 1. Принципы построения и функционирования микроэвм
Лекция 2. Память микроэвм. Средства реального времени
Лекция 3. организация процесса обработки данных в микропроцессоре и микроэвм
Лекция 4. Структура МПСУ. Адаптеры датчиков и исполнительных механизмов
Лекция 5. Принципы реализации на микроэвм функций регулятора
Лекция 6. Стандартные интерфейсы периферийных устройств микроэвм
Лекция 7. Микропроцессорные системы централизованного контроля. Блок SAU 8800
Лекция 8. Принципы построения судовых МПСУ
Лекция 9. Судовая МПСУ " Data chief-7 "
Лекция 10. Судовая МПСУ " Data chief-C 20"
Лекция 11. Микропроцессорная система управления двигателей серии МЕ фирмы MAN B&W
Лекция 12. Принципы построения систем питания
Лекция 13. Основы технического обслуживания микропроцессорных систем
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 886; Нарушение авторских прав?; Мы поможем в написании вашей работы!