Расчет параметров сетевого графика

Параметрами сетевого графика называются величины, характеризующие положение работ и событий, которые дают возможность проанализировать состояние работ и принять необходимые решения. Исходными для определения всех временных параметров сетевых моделей служит продолжительность работы (t_ij). На основании продолжительности работ в сетевом графике определяются его временные параметры, основными из них являются следующие.

3.1. Продолжительность пути

,

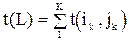где К - количество работ, входящих в данный путь.

Таким образом, продолжительность пути это суммарная продолжительность работ, составляющих данный путь.

Продолжительность критического пути

Т_кр = t[L(J-C)_max]

Продолжительность критического пути определяет срок наступления завершающего события сети, т. е. определяет срок выполнения проекта (планируемого комплекса работ) в целом.

3.2. Резерв времени пути - это разность между продолжительностью критического и данного пути. Он показывает на сколько в сумме могут быть увеличены продолжительности работ, принадлежащих данному пути, не изменяя срока выполнения проектов

R(L) = T_кр - t(L)

3.3. Ранний срок свершения события - срок, необходимый для выполнения всех работ, предшествующих данному событию i

Т_р(i) = t[L(J-i)_max] или Т_р(j) = [T_p(i) + t_ij]^max

Ранний срок исходного события сети принимается равным нулю

Т_р(J) = 0

3.4. Поздний срок свершения события - это наиболее поздний из допустимых сроков свершения события, превышение которого на какую-то величину вызывает аналогичную задержку наступления завершающего события

Т_п(i) = T_кр - t[(i-C)_max] или Т_п(i) = [Т_п(j)-t_ij]^min

Поздний срок завершающего события равен его раннему сроку Т_п(С)=Т_р(С), это же имеет место и для событий, лежащих на критическом пути Т_р(i) = Т_п(i).

3.5. Резерв времени свершения события - это такой предельно допустимый срок, на который можно задерживать свершение данного события, не вызывая при этом увеличения продолжительности критического пути (т. е. не изменяя срока свершения завершающего события), т. е. всего проекта в целом.

У событий, лежащих на критическом пути, резервов времени не существует. Резерв времени события определяется следующим образом:

R(i) = T_п(i) - T_p(i) = R(L_max)

Резерв времени события равен резерву времени максимального из путей, проходящих через данное событие.

3.6. Ранний срок начала работы - это самый ранний из возможных сроков начала работы:

t_р.н.(ij) = T_p(i)

3.7. Ранний срок окончания работы - это самый ранний из возможных сроков окончания работы:

t_р.о.(ij) = t_р.н.(ij) + t_ij = T_p(i) + t_ij

3.8. Поздний срок начала работы - самый поздний срок начала работы, при котором не увеличивается продолжительность критического пути, т. е. срок окончания проекта в целом:

t_п.н.(ij) = t_п.о.(ij) - t_ij = T_п(j) - t_ij

3.9. Поздний срок окончания работы - самый поздний срок окончания работы, при котором не увеличивается продолжительность критического пути, т. е. срок окончания проекта:

t_п.о.(ij) = T_п(j)

Для работ критического пути:

t_р.н.(ij) = t_п.н.(ij) и t_р.о.(ij) = t_п.о.(ij)

3.10. Полный резерв времени работы - это величина резерва времени максимального из путей, проходящих через данную работу. Он равен разности между поздним сроком наступления события и ранним сроком наступления события за вычетом продолжительности работы

R_п(ij) = T_п(j) - T_p(i) - t_ij

Полный резерв времени работы показывает, на сколько может быть увеличена продолжительность отдельной работы или отсрочено ее начало, чтобы продолжительность проходящего через нее максимального пути не превысила продолжительности критического пути (т. е. чтобы не изменился срок выполнения проекта в целом).

Использование полного резерва целиком на данной работе отнимает все полные резервы времени у работ, лежащих на всех путях, которые проходят через данную работу.

Полный резерв времени работ критического пути равен нулю, а для остальных работ он положителен.

3.11. Свободный резерв времени работы - равен разности между ранними сроками наступления событий j и i за вычетом продолжительности работы (ij):

R_c(ij) = T_p(j) - T_p(i) - t_ij

Свободный резерв представляет собой часть полного резерва времени работы. Он указывает максимальное время, на которое можно увеличить продолжительность отдельной работы, или отсрочить ее начало, не меняя ранних сроков начала последующих работ, при условии, что непосредственно предшествующее событие наступило в свой ранний срок.

В качестве плановых сроков начала работ берутся при этом ранние сроки наступления событий. Сводный резерв времени является в определенном смысле независимым резервом, т. е. использование его на одной из работ не меняет величины свободных резервов времени остальных работ сети.

3.12. Коэффициент напряженности работы используется в сетевом планировании для характеристики напряженности сроков выполнения работ и определяется по следующей формуле:

,

где t(L_max) - продолжительность максимального пути, проходящего через данную работу;

t¢(L_кр) - продолжительность отрезка пути t(L_max), совпадающего с критическим путем.

С помощью коэффициента напряженности получают оценку напряженности работ, лежащих на путях равной продолжительности и обладающих одинаковыми резервами времени.

Величина коэффициента напряженности у разных работ в сети лежит в пределах 0 Í К_н(ij) Í i.

Для всех работ критического пути К_н(ij) = 1.

Величина коэффициента напряженности помогает при установлении плановых сроков выполнения работ оценить, насколько свободно можно располагать имеющимися резервами времени. Этот коэффициент дает исполнителям работ предоставления степени срочности работ и позволяет установить очередность их выполнения, если она не определяется технологическими связями работ.

Дата добавления: 2014-01-06