Лекция №13 Полигауссовы модели случайных воздействий и методы их анализа

Вопросы

1. Каким образом определяется точность САУ?
2. Какое влияние на работы системы оказывают случайные воздействия?
3. Можно ли считать что в реальных САУ все процессы детерминированы?
4. Какими могут быть случайные процессы, воздействующие на систему?
5. Что понимают под белым шумом?

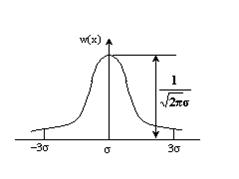
Рисунок 13‑1 Гауссовское распределение

Точка перегиба, в которой кривая распределения имеет максимальную крутизну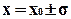

Случайный гауссовский процесс имеет очень важное свойство: при прохождении через линейные цепи, форма распределения не изменяется, а могут изменяться только его параметры.

А поскольку в автоматике и системах автоматического управления линейные цепи являются основными, то и аппарат гауссовских распределений адекватен задаче курса. В последнее время при более точном анализе случайных процессов было выявлено много примеров, когда случайный процесс не является гауссовским, а имеет произвольную форму. В этом случае прибегают к аппарату полигауссовых законов распределений. Случайный процесс называют полигауссовским, если соответствующая функция распределения вероятностей представляется смесью полигауссовых законов распределения.

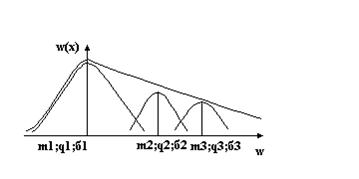
Рисунок 13‑2 Полигауссовское распределение

При анализе линейных цепей полигауссовский закон распределения позволяет произвольно аппроксимировать смесью гауссовских, провести схему для каждой компоненты гауссовского закона, а в итоге, отклики по каждой компоненте сложить и получить результирующий отклик линейной системы на произвольное распределение.

Реализацию случайного процесса с полигауссовским распределением можно представить в виде:

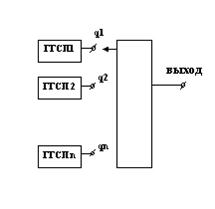
Рисунок 13‑3 Случайный процесс полигауссовского распределения

Марковские модели случайных процессов.

Случайный процесс, который описывается совместным распределением двух от счетов, называется Марковским.

Рисунок 13‑4 Марковское распределение

Марковские случайные процессы играют такую же роль, как и гауссовские процессы, находят широкое применение в теории случайных явлений.

Взаимоотношения между Марковскими, гауссовыми и полигауссовыми случайными процессами представляются на диаграмме случайных процессов:

Рисунок 13‑5 Диаграмма случайных процессов

Ось моментов - число начальных моментных функций, которое может быть использовано для описания того или иного случайного процесса.

Гауссовским процессам на этой диаграмме соответствует пара горизонтальных прямых, показывающих, что гауссовская модель описывается двумя первыми моментами для любого множества точек на оси времени.

Марковские процессы представлены также парами, но уже вертикальных прямых. Для любых двух точек на оси времени определяется любое множество моментов.

Рассмотрим несколько примеров прохождения случайных процессов через типовые линейные звенья.

Дата добавления: 2014-01-06