Табулирование функции одной переменной

Циклы

Циклы применяются для решения самых разнообразных задач:

- табулирования функций;

- определения экстремумов функций;

- вычисления сумм конечных и бесконечных рядов;

- вычисления определенных интегралов;

- решения алгебраических и трансцендентных уравнений численными методами;

- операций с матрицами;

- автоматизированный ввод и вывод данных.

Редкая вычислительная процедура обходится без использования циклов.

Под табулированием понимают конструирование или вычисление (составление) различных математических таблиц.

Наиболее широко этот метод использовался до появления вычислительной техники. Например, для вычисления значений тригонометрических функций, интегралов широко использовались таблицы, рассчитанные в научных центрах и представленные в виде таблиц. Табличные методы задания функций могут применяться и в малых вычислительных машинах для сокращения времени вычисления с использованием методов интерполяции и экономии памяти, необходимой для хранения сложных программ вычисления по точным формулам. Табулирование может применяться также для построения графиков функций.

Суть табулирования функции состоит в том, что весь диапазон изменения независимой переменной разбивают на равные интервалы и для каждого значения аргумента в граничных точках интервалов (узлах интерполяции) вычисляется значение функции одним из известных методов с требуемой точностью. Результаты расчетов представляются в виде таблицы, в одной из колонок которой приводятся значения аргумента, а в другой - соответствующее ему значение функции. Алгоритм расчета представляет собой цикл типа "До", так как число шагов обычно известно заранее, или сочетание циклов "До" и "Пока", если заданы требования к точности вычислений.

Пример 8.3.6. Составить таблицу значений функции y= x²+2x -4 для х, изменяющегося в диапазоне от 0 до 10 с шагом 0,5.

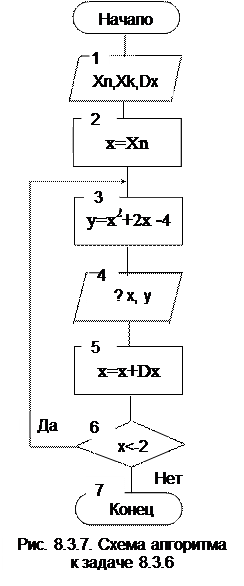
Решение. Введем обозначения: Xn – начальное значение аргумента, Xk – конечное значение аргумента, Dx – шаг приращения аргумента. Программа работает следующим образом (рис. 8.3.7):

Блок 1. Вводим исходные данные: Xn, Xk, Dx.

Блок 2. Присваиваем текущему значению аргумента х начальное значение Xn.

Блок 3. Вычисляем значение функции при текущем значении аргумента.

Блок 4. Выводим на экран или печать значения x и y.

Блок 5. Увеличиваем значение аргумента на величину шага.

Блок 6. Проверяем условие окончания цикла. Если условие выполняется, то есть текущее значение аргумента меньше конечного значения аргумента, то возвращаемся на блок 3 и повторяем вычислительную процедуру (блоки 3, 4, 5, 6).Если условие не выполняется, то конец программы.

алг Табулирование_функци

дано Xn, Xk, Dx

нц для х от Xn до Xk с шагом Dx

y = x²+2x -4

рез x, y

кц

кон

Пример 8.3.7. Вычислить сумму и произведение чисел натурального ряда от 2 до 100.

Решение. Введем обозначение Xn – начальное значение аргумента, N – число членов ряда, Dx – шаг, S – сумма чисел, P – произведение чисел.

алг Вычисление суммы

дано Xn, N

нач

S=0

P=1

нц для i от Xn до N с шагом Dx

S=S+i

P=P*i

кц

рез S, P

кон

В данном алгоритме (рис. 8.3.8) для вычисления суммы чисел переменной S до входа в цикл присваивается начальное значение нуль S=0, а для вычисления произведения переменной P присваивается начальное значение единица Р=1. В теле цикла проводится вычисление S: к текущему значению суммы прибавляется текущее значение переменной цикла S=S+i. Для вычисления произведения текущее значение произведения Р умножается на текущее значение переменной цикла – P=P*i.

Данный алгоритм не отвечает свойству массовости, так как не позволяет вычислять отдельно сумму четных или нечетных чисел. Чтобы обеспечит такую возможность, необходимо формировать запрос, что надо подсчитать. Кроме того, необходимо обеспечить контроль значения Xn, так как при вычислении произведения чисел Xn не может быть равным нулю, при вычислении суммы или произведения четных чисел начальное значение Xn должно быть четным, а при вычислении суммы или произведения нечетных чисел – нечетным.

Проверить четность числа можно с помощью функции MOD. Функция MOD вычисляет отношение двух целых чисел и возвращается значение 0, если остаток от деления равен нулю, то есть число четное, и возвращает значение один, если остаток от деления не равен нулю, то есть число нечетное. Например: 5 MOD 2, - результат 1).

Пример 8.3.8. Найти приближенное значение глобальных экстремумов функции y=F(x) на отрезке [A,B].

Решение. Задача решается путем табулирования функции с некоторым, достаточно малым шагом. На каждом шаге табулирования выполняется сравнение вычисленного значения функции с некоторой переменной, принятой за максимум и, если значение функции больше этой переменной, то переменной присваивается значение функции. Аналогично выполняется поиск минимума.

Введем две переменные YMax и YMin. В качестве начального значения для переменной YMax можно взять большое отрицательное число, например -1Е38, а для переменной YMin – большое положительное число - +1Е38. В качестве начальных значений переменных YMax и YMin можно принять также значение функции на одной из границ отрезка табулирования функции.

Присвоим переменным YMax и YMin значения, равные значению функции в точке А отрезка табулирования функции.

Алгоритм поиска минимума и максимума функции:

алг Поиск_мин_мах

дано A, B, Dx

нач

Ymax= F(A): YMin=F(A)

нцдля x от A до B+Dx/2 с шагом Dx

y=F(x)

если y>Ymax

то YMax= y

все

если y<YMin

то YMin= y

все

кц

рез YMax, YMin

кон

В данном примере y=F(x) - любая заданная функция.

Так как шаг табулирования выбирается произвольно, то можно потерять значение функции на конце отрезка. Чтобы этого не произошло, условием окончания цикла принимается не B, а B+Dx/2. Схема алгоритма во многом будет похожа на схему, представленную на рис. 8.3.8 только в тело цикла включаются проверки значений функции на минимум и максимум.

Пример 8.3.9. Составить таблицу значений функции е^х для заданного значения х с точностью 0,0001.

Решение. Функцию e^x, можно представить в виде ряда

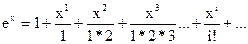
или

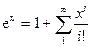, (8.3.3)

Данный ряд сходящийся. Под точностью в данном случае понимается значение отбрасываемого члена ряда. Полная ошибка может быть в несколько раз больше значения отбрасываемого члена ряда. Для знакопеременных рядов ошибка вычисления суммы сходящегося ряда не превышает значения отбрасываемого члена ряда.

Алгоритм вычисления функции реализуется с помощью цикла типа "Пока" (рис.8.3.9).

Первый блок вводит исходные данные: x - значение аргумента и Е — точность вычисления значения текущего члена ряда. Вто­рой и третий блоки осу­ществляют начальное присвоение переменной цикла, S – начальное значение суммы, Р – вспомогательная переменная для вычисления факториала. Начальное значение суммы равно единице, так как в выражении 8.3.3. имеется соответствующее слагаемое. Начальное значение y также принимаем равным 1+Е, чтобы на первом шаге программа вошла в цикл. Четвер­тый блок проверяет условие окончания цикла – достижение заданной точности вычисления текущего члена ряда. Если условие выполняется, то выполняется тело цикла, иначе осуществляется переход на блок 7 – печать результата и выход из программы – блок 8. Пя­тый блок обеспечивает вычисление значения функции: вычисляется текущее значение факториала - Р, значение текущего члена ряда – Y, и значение функции на текущем шаге – S.

С точки зрения вычислительной математики блок 5 построен нерационально, так как на каждом шаге необходимо вычислять выражение xⁱ/(i!), кроме того, при больших значениях i наступает переполнение разрядной сетки. Скорректируем математическую модель:

, (8.3.4)

В данной модели степень переменной x заменена ее произведением, а в числителе факториал заменен произведением ряда натуральных чисел от единицы до i. При такой модели значение текущего элемента будет равно значению предыдущего элемента умноженного на x и деленного на i.

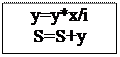С учетом сделанных замечаний блок 5 алгоритма (рис. 8.3.8) будет вы

глядеть следующим образом:

Данный пример показывает, как от правильного построения математической модели зависит эффективность алгоритма.

Контрольные вопросы и упражнения

1. Назовите основные этапы жизненного цикла программы.

2. Охарактеризуйте основные этапы жизненного цикла программы.

3. Приведите определение алгоритма, назовите и поясните основные свойства алгоритма.

4. Что такое нисходящая разработка?

5. Что такое модуль, в чем заключается особенность модульного проектирования?

6. В чем состоит особенность структурного программирования?

7. Изобразите основные элементы схем алгоритмов.

8. Изобразите базовые схемы алгоритмов.

9. Опишите базовые структуры на алгоритмическом языке.

10. Изобразите структуру линейной программы.

11. Пусть S= -1, если x<0; S=0, если x=0; S=1, если x>0. Опишите решение задачи на алгоритмическом языке и с помощью схемы алгоритма.

12. Разработайте схему алгоритма для решения квадратного уравнения в области действительных чисел.

13. Протабулируйте функцию y=Sin(x)+1/x² на отрезке [-3,14; 3,14] и найти максимум функции. Описать решение задачи на алгоритмическом языке и с помощью схемы алгоритма.

14. Разработайте алгоритм для печати таблицы умножения.

15. Разработать алгоритм программы для суммирования штрафного времени при игре в хоккей.

16. Разработать схему алгоритма программы для печати результатов соревнования по плаванью. В заплыве плывут М спортсменов. На экран выводить список участников заплыва в порядке показанных результатов. На экран выводить также мировой и европейский рекорды, а также фамилии участников заплыва, превысивших эти рекорды.

17. Разработать схему алгоритма для определения дальности полета снаряда. Известна высота орудия, начальная скорость стрельбы и угол стрельбы.

Дата добавления: 2014-01-06