Приближенный поиск экстремумов

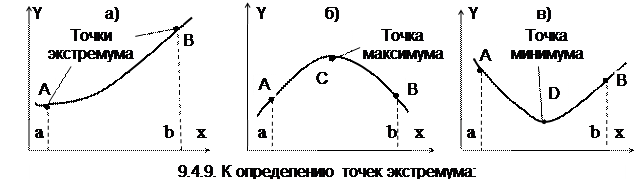
Во многих задачах вычислительной математики требуется найти максимальное или минимальное значение функции (экстремум) на заданном отрезке [а; b]. Эк­стремум может находиться на концах отрезка (рис. 9.4.9 a) или внутри отрезка. Функция может быть выпуклая (выпуклая вверх) (рис. 9.4.9 б) или вогнутая (выпуклая вниз) (рис.9.4.9. в). Имеются простые способы анализа функций на отрезках, основанные на определении зна­ка первой и второй производной.

Если функция непрерывна на отрезке, то:

если первая производная f' (x) не меняет знак на концах отрезка, то функция является монотонно убывающей, если f' (x) < 0, и возрастающей, если f’ (х) > 0. Монотонные функции достигают экстремума на концах отрезка;

если на концах отрезка производная функции меня­ет знак, то экстремум находится внутри отрезка. При­чем, если вторая производная больше нуля, то в точке экстремума функция достигнет минимума. Если вторая производная меньше нуля, то в точке экстремума фун­кция достигает максимума.

Поиск экстремума функции внутри отрезка может быть выполнен с помощью табулирования функции. Для этого достаточно в процессе табулирования сравнивать текущее значение функции с переменной, значение которой принято за максимум (минимум).

Если на отрезке один экстремум, то наиболее эффективным методом поиска будет один из методов одномерной поисковой оптимизации. Для этой цели могут быть использованы те же методы, что и для уточнения корней: метод дихотомии, "золотого се­чения", простых итераций.

Пример9.4.13. Проанализировать функцию у = 5х² - 8х + 1 на отрезке

[-1+1].

Решение. Находим первую производную функции y:

у' = 10 x - 8; у'(а) = -18; y'(b) = 2.

Функция имеет экстремум на заданном отрезке, так как первая производная на концах отрезка меняет знак. Вторая производная функции у" = 10, то есть боль­ше нуля. Следовательно, функция имеет на отрезке [-1; 1] точку минимума.

Метод "золотого сечения"

В отличии от метода итераций, метод "золотого сечения" не требует задания начального значения корня. Достаточно указать требуемую точность поиска. В этом методе отрезок отделения [а; b] делится на неравные части. Одна точка (D) задается на расстоянии 0,618, а другая (C) – на расстоянии 0,382 длины отрезка [а; b] от точки а (рис. 9.4.9) и определяют, в какой из точек С или D производная функции меняет знак по отношению к знаку производной от этой функции в точке а. Если в точке D производная функции знак не меняет, то сразу переходят к анализу отрезка [d, b].

Если в точке d производная функции меняет знак, то проверяют значе­ние производной функции в точке c. Если в точке c производная функции знак не меняет, то переходят к анализу отрезка [c,d], в противном случае анализируют отрезок [а, c]. Данный метод обеспечивает более быструю сходимость, чем метод дихотомии и метод итераций.

CLS

REM Определение экстремума функции методом золотого сечения

DEF fnf (x) = COS(x ^ 2) * 2

DEF fnf1 (x) = SIN(x ^ 2) +.5

INPUT "Введите границы отрезка А и В", a, b

INPUT "Укажите требуемую точность Е ", e

k = b

m1:

'CLS

c = a +.382 * (b - a): d = a +.618 * (b - a)

y = fnf(a) ' fnf – функция пользователя

y1 = fnf(b)

'PRINT a, c, d, b

PRINT y, y1

IF b - a < e THEN x = (b + a) / 2: PRINT "экстремум: "; x, "f'(b)="; y1, "f(b)="; fnf1(x): END

b = c: y1 = fnf(b)

IF y * y1 < 0 THEN GOTO m1

a = c: b = d: y = y1: y1 = fnf(b)

IF y * y1 < 0 THEN GOTO m1

a = d: b = k: y = y1: y1 = fnf(b)

IF y * y1 < 0 THEN GOTO m1

x = b:

PRINT "экстремум: "; x, "f'(b)="; y1, "f(b)="; fnf1(x)

END

Дата добавления: 2014-01-06