
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Следствия из основной теоремы зацепления
|
|
|
|
Если зацепление правильное, то есть контакт между профилями не нарушается, то общая нормаль к профилям, проведенная через точку их контакта, делит межосевое расстояние на отрезки, обратно- пропорциональные угловым скоростям звеньев.
Правильным называется такое зацепление, в котором контакт профилей существовал до рассматриваемого момента, существует в рассматриваемый момент и будет существовать после рассматриваемого момента.
Под зацеплением понимают высшую кинематическую пару (т.е. контакт двух материальных тел по линии или в точке), в которой движение от одного тела к другому передается путем давления (или за счет сил давления).
Основная теорема плоского зацепления
(Основной закон. Теорема Виллиса)
Понятие зацепления шире, чем контакт зубчатых колес. Это может быть и контакт кулачка с роликом, кулачка с толкателем, контакт двух любых криволинейных поверхностей.
Мы будем рассматривать плоское зацепление. Плоским называется такое зацепление, в котором относительное движение звеньев плоское (в одной плоскости или параллельных плоскостях).
Основная теорема зацепления устанавливает связь между кинематикой звеньев (угловыми скоростями) и геометрией контактирующих поверхностей (их формой).
Теорема справедлива для любых двух звеньев, передающих движение силой давления, т.е. для любой кинематической пары, где движение передается силой давления.
Рассмотрим случай, когда оба контактирующих тела совершают вращательное движение. Это частный случай плоскопараллельного движения. В планетарных механизмах, например, сателлиты совершают плоскопараллельное движение.
Пусть два произвольных профиля контактируют в данный момент времени в точке А (рис. 1). При этом звено I совершает вращательное движение вокруг оси O1 с угловой скоростью w1 и передает движение звену 2, которое вращается с угловой скоростью w2 вокруг оси О2. Зацепление будем считать правильным.
Определим передаточное отношение от звена 1 к звену 2.
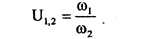
Рассмотрим, как передаточное отношение связано с формой контактирующих поверхностей, с геометрией зацепления. Определим линейные скорости точки А, как принадлежащей звену 1 и звену 2. Для этого соединим центры вращения O1 и О2 с точкой контакта звеньев А. Полученные отрезки O1A и О2А, проведенные в мгновенную точку контакта, являются мгновенными радиусами вращения. Поэтому абсолютные скорости точек A1 и А2 направлены перпендикулярно к соответствующим радиусам вращения.
|
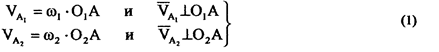
Так как точка А расположена не на межосевой линии O1 и O2, то линейные скорости точек 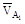 и
и 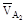 не совпадают по направлению. Это общий случай.
не совпадают по направлению. Это общий случай.
Через точку контакта профилей проведем общую нормаль n-n и большую касательную t-t к профилям и спроектируем на них абсолютные скорости точек 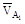 и
и 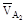 . Обозначим проекции скоростей на общую нормаль n-n соответственно C1 и С2, а на общую касательную t-t соответственно K1 и К2.
. Обозначим проекции скоростей на общую нормаль n-n соответственно C1 и С2, а на общую касательную t-t соответственно K1 и К2.
Точку пересечения нормали n-n с межосевой линией обозначим Р. С центров вращения O1 и О2 на общую нормаль проведем перпендикуляры O1B1 и О2В2. Углы между направлениями скоростей 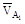 и
и 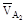 и общей нормалью обозначим соответственно g1 и g2. Проанализируем связь между проекциями скоростей
и общей нормалью обозначим соответственно g1 и g2. Проанализируем связь между проекциями скоростей 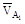 и
и 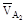 на общую нормаль C1 и С2. Поскольку отрезки, изображающие векторы
на общую нормаль C1 и С2. Поскольку отрезки, изображающие векторы 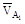 и
и 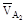 , мы выбрали произвольно не определяя их точно, то возможны следующие соотношения между C1 и С2:
, мы выбрали произвольно не определяя их точно, то возможны следующие соотношения между C1 и С2:
1. Предположим, что C1<C2. Тогда профиль 2 уйдет от профиля 1 и зацепление нарушится, т.е. пере-станет существовать кинематическая пара. Следовательно по условию правильного зацепления проекция 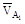 на общую нормаль C1 не может быть меньше проекции
на общую нормаль C1 не может быть меньше проекции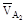 на общую нормаль С2.
на общую нормаль С2.
2. Предположим, что C1>C2. Тогда в процессе работы профиль 1 должен обогнать профиль 2, что возможно только при деформации профиля 2 или профиля 1, что по условиям работы кинематической пары недопустимо. Следовательно С1 не может быть больше С2.
|
|
|


3. Таким образом остается единственный правильный вариант
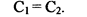
Только при этом условии может существовать кинематическая пара 1 -2.
Изобразим отдельно кинематическую пару 1-2 с соблюдением этого условия (рис. 2). Запишем условие C1 = C2 через абсолютные скорости точек профилей

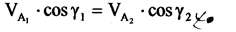
|
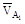 и
и 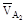 по уравнениям (1)
по уравнениям (1)
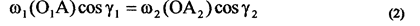
|







|

Рассмотрим полученное равенство. Здесь левая часть 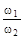 характеризует кинематику зацепления - пе-
характеризует кинематику зацепления - пе-
редаточное отношение. Правая часть 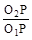 характеризуют геометрию контактирующих поверхностей (про-
характеризуют геометрию контактирующих поверхностей (про-
филей), так как положение общей нормали целиком и полностью зависит от геометрии профилей. Таким образом мы получили аналитическую зависимость между геометрией контактирующих профилей и их кинематикой.
Это и есть основная теорема зацепления.
1. Для постоянства передаточного отношения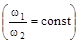 , необходимо чтобы отношение отрезков
, необходимо чтобы отношение отрезков 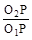
было постоянным, а это возможно, если межосевое расстояние O1O2 неизменно и точка Р должна занимать на межосевой линии одно и то же положение. Это теоретически возможно в двух случаях:
а) нормали к контактирующим профилям в процессе зацепления образуют пучок прямых, проходящих через точку Р-полюс зацепления (рис. 3 а); это свойство используется в циклоидальном зацеплении (применяется в механизмах приборов, часовых механизмах);
б) линия нормали занимает неизменное положение, а точка контакта профилей перемещается вдоль неё (рис. 3 б); это свойство характерно для зацепления эвольвентных профилей.
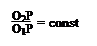

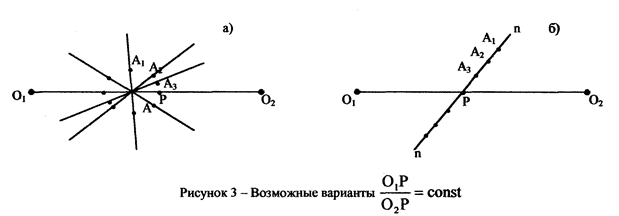
2. Проекции скоростей точек контакта звеньев на общую касательную t-t не равны при равенстве проекций на общую нормаль n-n: K1¹К2 при С1 = С2. А это значит, что профили при движении проскальзывают. Это явление безусловно отрицательное, поскольку происходит износ профилей. При проектировании передач проскальзывание профилей стараются уменьшить.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1541; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 . Они подобны, так как их стороны взаимно перепенди-
кулярны. Тогда Ð АО1В1 =
. Они подобны, так как их стороны взаимно перепенди-
кулярны. Тогда Ð АО1В1 = 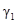 .
Аналогично подобны и треугольники О2В2А и
.
Аналогично подобны и треугольники О2В2А и  и Ð АО2В2 =
и Ð АО2В2 = 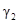 . Из треугольников
АО1В1 и АО2В2 получим
. Из треугольников
АО1В1 и АО2В2 получим