
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы доказательства тавтологии
|
|
|
|
Если каждая элементарная сумма, входящая в КНФ, содержит хотя бы одно высказывание вместе со своим отрицанием, то данная формула- тавтология.
В нашем примере так оно и есть, т.е. данная формула ─ тавтология
Таким образом, чтобы установить, к какому виду относится данная формула, нужно ее привести к ДНФ и КНФ.
1. Таблица истинности.
2. Приведение к КНФ.
3. Метод от противного.
Сущность 3-го метода заключается в том, что предполагается истинность противоположного утверждения, и на основании анализа формул мы получаем заключение о том, что она противоречит предположению. Это является доказательством того, что предположение ложно.
Пример:
Пусть имеется формула (p q)(q
q)(q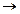 r)
r) 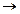 (р
(р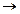 r).
r).
Предположим, что эта формула не является тавтологией. Это значит, что существует некоторый набор значений элементарных высказываний, при котором левая часть импликации истинна, а правая ложна. Пусть это: р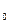 , q
, q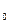 , r
, r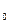
Получим систему
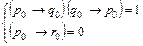 отсюда:
отсюда: 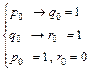
Из 3-его имеем р0 = 1. Тогда из 1 получим q0 = 1, а из 2 получим r0 = 1.
В результате r  = 1 и r
= 1 и r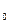 = 0.
= 0.
Мы пришли к противоречию, следовательно, наше предположение ложно и формула – тавтология.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 3622; Нарушение авторских прав?; Мы поможем в написании вашей работы!