Предикаты

При анализе рассуждений в логике высказываний нас не интересовала внутренняя структура самих высказываний. И это обстоятельство не позволяет анализировать большое количество рассуждений.

Примеры:

1. Через две данные точки проходит единственная прямая.

2. Точка лежит между двумя точками.

3. х > 5.

Эти предложения не являются высказываниями, но становятся таковыми, если предметным переменным, входящим в эти предложения, задать конкретны значения. Так, в последнем примере при х = 3 получим ложное высказывание, а при х = 8 истинное высказывание. Значения предметных переменных берутся из некоторого предметного множества А (точек, углов, прямых, чисел, ромбов и т.д.).

Введем понятие предиката.

Под предикатом предметной переменной х 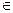А будем понимать функцию Р (х) на {0,1}. Предикат Р (х) называется одноместным предикатом

Например:

Предикат х > 5, x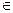R: при х = 4 предикат обращается в ложное высказывание. При х = 7 предикат обращается в истинное высказывание.

Функция Р (х, у), где х, у 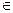А, принимающая значения во множестве {0,1} называется двухместным предикатом.

Например: х < у

Пусть у = 5, получим х < 5 – одноместный предикат. Если положить х = 4, то 4 < 5 – нульместный предикат (высказывание).

Местность предиката ─ количество предметных переменных. Задание конкретного значения предметным переменным понижает местность предиката. Одноместные предикаты выражают свойство быть чем-то.

Например:

Свойство быть точкой. х – точка. Введем обозначение этого предиката: Т (х). Тогда Т (А) читается как А ─ точка.

Двухместные предикаты и предикаты более высокой местности выражают отношения между объектами.

Например:

Двухместный предикат принадлежности – х 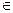у. Если х – точка, а у – прямая, то читаем: точка х принадлежит прямой у.

Выбор предикатного символа остается за пользователем. Так, вместо х 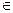у можно ввести предикат Р (х, у), оговорив, что Р (,) – это предикат принадлежности (запятая в скобках свидетельствует о том, что предикат двухместный). Разумеется, что нельзя использовать одно и тоже обозначение для разных предикатов. Широко используются известные из математики обозначения предикатов ≈, ≠, ≡, ≤, ≥, ┴, _║,=

Дата добавления: 2014-01-06