Смежность

Графы

Помехоустойчивое кодирование

При кодировании сообщений, как правило, происходит передача закодированных сообщений. При этом в канале связи могут возникать помехи, в результате которых на выходе получается искаженное сообщение, что затрудняет его декодирование. Помехи бывают четырех видов:

1) Замена бита на другой бит.

2) Удвоение разряда.

3) Потеря разряда.

4) Комбинация этих помех.

Все зависит от технических характеристик канала связи.

Предположим, что канал связи таков, что для сообщения длины n – битов, в нем происходит одна ошибка замещения бита. Тогда можно произвести кодирование так, что возникшие ошибки могут быть исправлены автоматически.

Одним из способов исправления таких ошибок является, так называемый, «способ голосования», то есть каждый бит заменяется тремя одинаковыми битами. И на выходе всё сообщение разбивается на тройки. Может оказаться, что в какой-то тройке два бита одинаковые, а третий нет. Следовательно, отличающийся бит неправильный. Его можно исправить.

Таким образом, вся цепочка передачи сообщения может иметь вид:

Сообщение – составление алфавита А и выявление частоты появления каждой буквы – упорядочивание алфавита по убыванию частот – кодирование – утроение каждого бита – передача кода по каналу связи – разбиение кода на тройки – исправление ошибок – сброс лишних бит – декодирование.

Существуют и другие методы помехоустойчивого кодирования.

Задача:

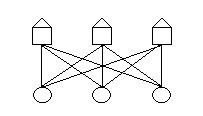Имеется 3 домика и 3 колодца. От каждого домика к каждому колодцу проложена тропинка. Требуется проложить тропинки так, чтобы они не пересекались.

Рис. 22. Три домика, три колодца

Эта задача решений не имеет.

Польский математик Куратовский и советский математик Понтрягин независимо друг от друга в 1930 году доказали, что при решении этой задачи хотя бы одно пересечение будет. 6.1. Понятие графа

Рассмотренная задача относится к числу классических задач теории графов, в создании которой приняли люди самых разных профессий: математик Эйлер, химик Кэли, физик Кирхгоф….

Определение.

Пусть задано некоторое множество V= { V,V,…,V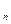 }. Образуем множество Е, элементами которого являются неупорядоченные пары, составленные из элементов множества V: Е ={(V ,V ), (V,V )….}, причем (V,V ) = (V,V ). Множество V называется множеством вершин, а множество Е – множеством ребер. Совокупность этих множеств называется графом G(V,E).

Очень широкое распространение получило изображение графа в виде диаграммы, в которой вершины изображаются точками, а ребра – линиями (необязательно прямыми).

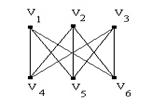
Рис. 23. Граф Понтрягина - Куратовского

Если вершина V принадлежит ребру е , то V и е называются инцидентными.

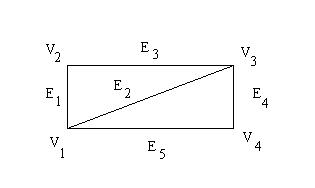Две вершины, инцидентные одному ребру, называются смежными. Два ребра, инцидентные одной и той же вершине, тоже называются смежными.

Рис.24. Пример графа

Вершина V₁ смежна с вершинами V₂ и V_{4 .} Ребро Е ₁ является смежным с ребрами Е₂, Е₃, Е₅.

Количество ребер, инцидентных данной вершине, называется степенью вершины - d(V).

Например, для рис. 24 имеем d (V ) = 3, а d (V ) = 2.

Если d(V) = 0. то вершина называется изолированной. Если d (V)=1, то вершина называется висячей или концевой.

Если все вершины графа имеют одинаковую степень к, то граф называется регулярным степени к.

Рис. 25. Регулярный граф степени 3

Дата добавления: 2014-01-06