Изоморфизм

Над графом можно производить различные действия: добавить, удалить ребро / вершину, изменить направление ребра ит.д.

Два графа называются изоморфными, если при преобразовании не нарушается смежность.

Пример изоморфных графов.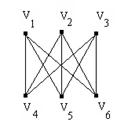

Рис. 27.. Граф 1 Рис. 28. Граф 2.

В самом деле, вершинам V_1, V₂, V₃ смежными в обоих графах являются вершины V₄, V_5, V₆. Вершинам V₄, V_5, V₆ смежными в обоих графах являются вершины V_1, V₂, V_{3 ,} что и доказывает их изоморфизм_.

Чтобы установить изоморфизм двух графов надо перебрать все возможные способы расстановки смежных вершин. Если существует хотя бы один способ, устанавливающий одинаковую смежность, то графы изоморфны. Если такого соответствия нет, то графы не изоморфны.

Рассмотрим граф

Рис. 29. Граф 3

Будет ли этот граф изоморфным графу 1? Количество вершин и ребер одинаково. Пусть V₁ - в левом верхнем углу. Тогда смежные вершины V₄, V₅, V₆ расположатся по соседним углам и в левой внутренней точке. Например, так

V₁ V₅

V₆

V₄

Рис. 30. Граф 3₁

Если вершину V₂ разместить в углу, то ока не будет смежна с V ₆. Если вершину V₂ разместить в средине, то ока не будет смежна с V₄. Ничего нового не будет, если разместить V ₁ в любом углу.

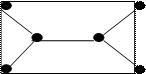
Разместим V₁ в средине. Тогда смежные вершины V₄, V₅, V₆ расположатся по углам и в средине.

V₆

V₁ V₅

V₄

Рис. 31. Граф 3₂

Если вершину V₂ разместить в углу, то ока не будет смежна с V ₆ , или с вершиной V₄.

Таким образом, разместить три несмежных вершины так, чтобы каждая из них была смежной с каждой из оставшихся не удается. Значит, граф 3 не изоморфен графу 1.

Дата добавления: 2014-01-06