Принцип максимума

Обозначим

Если 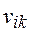- какая-либо система значений в узлах сетки и для каждого внутренних узла 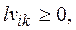то во внутренних узлах не могут иметь положительный максимум, а если во всех внутренних узлах 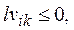то во внутренних узлах не могут иметь отрицательный минимум .

Исключением является случай

Доказательство (от противного).

Пусть и во всех внутренних узлах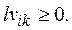

Предположим, достигает положительный максимум 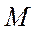в некотором внутреннем узле. Тогда можно найти внутренний узел 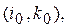в котором

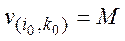и хотя бы в одном соседнем узле значение 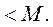Тогда

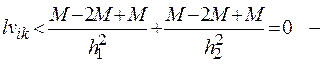получили противоречие с условием.

Теперь докажем, что система имеет единственное решение.

Для этого достаточнь показать, что однородная система имеет только тривиальное решение.

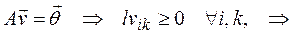можно применять принцип максимума,

то есть если хотя бы одно 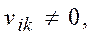то на границе должен быть либо положительный максимум, либо отрицательный минимум, что невозможно, т.к. 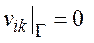по условию.

Значит, имеет только тривиальное решение 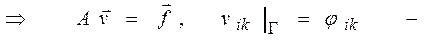только единственное решение.

Следующая задача – решить эту систему. Как уже отмечалось, матрица 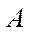имеет много нулей; такая матрица называется разреженной. Как правило, СЛАУ с такой матрицей решают методом итераций.

Для этого СЛАУ приводят к виду 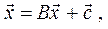выбирают начальное приближение и находят

и т.д.

Условие сходимости метода: (достаточное).

Рассмотрим случай, когда Тогда система примет очень простой вид:

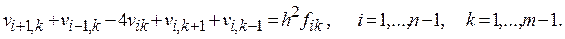
Имеем

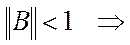сумма элементов в строке должна быть меньше 1,

у нас она = 1. Но поскольку это условие достаточное, то сходимость может быть.

Введем обозначения.

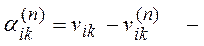погрешность решения на итерации.

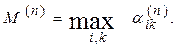
Разобъем узлы на разряды:

граничные узлы - узлы 1-го разряда: погрешность = 0;

узлы 2-го разряда-среди соседних есть узел 1-го разряда;

узлы 3-го разряда-среди соседних есть узел 2-го разряда и т.д.

То есть каждый узел попадает в один и только один разряд.

Из (1) вычитаем (2):

Для узлов 1-го разряда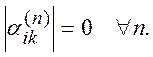

Для узлов 2-го разряда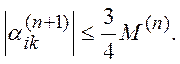

Для узлов 3-го разряда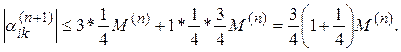

Для узлов 4-го разряда 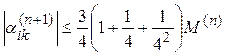и т.д.

Таким образом, 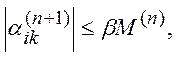где

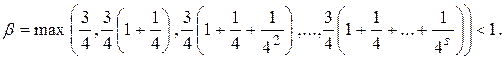
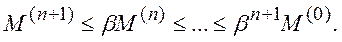
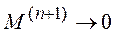Поскольку то при

Метод сходится.

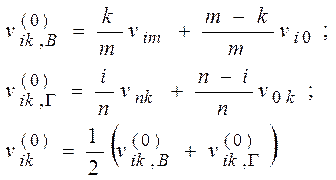
Дата добавления: 2014-01-06