Закон Кулона описывает формально взаимодействие заряженных тел, не раскрывая механизм этого взаимодействия

Электрическое поле. Наблюдаемое взаимодействие наэлектризованных тел объясняется тем, что каждое из них находится в электрическом поле, создаваемое другим наэлектризованным телом. При изменении заряда или при его перемещении, воздействие на второй заряд меняется не мгновенно, а с некоторым запозданием. Пространство, окружающее заряженной тело (электрическое поле) меняется, через это поле заряженное тело воздействует на другие заряженные тела. По этому воздействию электрическое поле обнаруживается, этим воздействием оно и характеризуется.

Электрическое поле в любой точке пространства характеризуется двумя физическими величинами – напряженностью и потенциалом.

Напряжённость электрического поля Е - это силовая векторная характеристика, численно равная силе, действующей со стороны поля на положительный единичный заряд, вносимый в поле. Если поле создано зарядом Q и в его поле вносится заряд q ₀, то напряжённость поля в данной точке:

Е = F / q ₀ (4). Если для данной точки поля известна напряжённость Е, тогда F = Е·q ₀ (5). Наглядно электрическое поле можно изобразить при помощи силовых линий. Силовые линии проводят так, чтобы касательные к ним в каждой точке совпадала с направлением вектора напряженности Е. Густота этих линий, пронизывающих единичную поверхность нормальную к линиям, равно численному значению вектора напряженности поля в этой области пространства. Электрические поля исследуются экспериментально и теоретически.

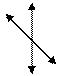
Рассмотрим некоторые примеры картины-спектра силовых линий поля точечного заряда (а), системы двух зарядов (б, в) и однородного поля (г):

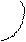
+q +q +q +q -q

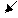а б в г

Используя закон Кулона (3) и формулу для напряженности (4), можно рассчитать напряженность поля точечного заряда q:

Е = F/q₀; F = kq ₀ q/r²; получим Е = kq/r² (6).

Если поле создано системой зарядов, то кулоновские силы и напряжённость реального поля определяются по правилу сложения векторных величин, т.е. выполняется принцип суперпозиции: Е = S E_i (7)

Часто встречаются случаи, когда поле создаётся двумя зарядами равными по величине и противоположными по знаку, расположенными на малом расстоянии друг от друга (например, полярные молекулы). Рассчитаем поле данной системы зарядов (q₁, q₂) в точке А (R, h, если h≪R)

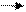Теорема Остроградского-Гаусса. Для удобства расчёта полей удобно пользоваться теоремой Остроградского-Гаусса: поток вектора напряжённости Е через любую замкнутую поверхность пропорционален суммарному заряду, расположенному внутри поверхности ∮Е_s dS = g/e_o (8)

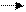Потенциал. Потенциал поля в данной точке j - энергетическая, скалярная характеристика электрического поля. Для её введения рассмотрим работу электрических сил при перемещении частицы с зарядом q из одной точки поля 1 в другую 2 (S). Работа, как и в механике) вычисляется по формуле A=FScosa. Как уже упоминалось, электрическое поле действует на заряд вносимый в поле, с силой F=Eq. Если напряжённость меняется, то работа вычисляется как А_1,2=∫ F_sdS= ∫ E_sqdS= = q∫ E_sdS = q j = q(j₂-j₁) = qU. Если-j₁ = 0, то А_1,2= q j₂, тогда j₂ = j = А_1,2/ q. j = А/ q ₀ (9)

Рассмотрим некоторые примеры.

1. Работа электрических сил по любому замкнутому контуру-пути равна нулю: А = q∮Е_s dS = 0. Циркуляция вектора напряжённости.

2. Если заряженная частица перемещается по поверхности перпендикулярной вектору Е и, следовательно, Е_s = 0, то работа электрического поля по перемещению заряда равна нулю А = 0 и разность потенциалов между любыми точками траектории перемещения равна нулю, т.е. точки поля имеют одинаковые потенциалы. Такая поверхность называется эквипотенциальной или поверхностью равного потенциала. Поверхность заряженного шара является эквипотенциальной поверхностью.

3. Для поля точечного заряда любая сфера является эквипотенциальной поверхностью, т.к. линии напряжённости – радиальные линии и перпендикулярные к шаровой поверхности. Для поля точечного заряда потенциал точек сферы

j = kq/r (10)

4. Используя понятие потенциала, можно рассчитать работу, совершаемую при переносе на поверхность шара заряда Q и, следовательно, энергию поля, созданного заряженным шаром. При переносе первой малой порции заряда dq на незаряженный шар электрические силы отсутствуют и работа равна нулю. При переносе следующих порций dq работа совершается против электрических сил заряженного шара. Пусть мы перенесли заряд q, потенциал шара пропорционален данному заряду j = aq. Работа по перемещению следующей порции dq будет равна dA=j dq=aq dq, а полная работа или энергия поля заряженного шара зарядом Q и имеющего потенциал j: А = ∫ dA = ∫ aQ dq = a∫ Q dq = a ∫ dQ²/2 = aQ²/2 = j Q/2, следовательно, А = W = j Q/2 (11)

Электроёмкость. Конденсатор. Как мы уже упоминали, заряженный проводник является эквипотенциальной поверхностью. Для заряженной проводящей сферы радиусом R₀, как и для сферы, окружающей точечный заряд Q₀, потенциал определяется формулой j₀ = kQ₀/R₀ (10), а отсюда отношение заряда к потенциалу Q₀/j₀ = R₀ /k = Cоnst. Для любого уединённого заряженного тела отношение заряда к его потенциалу остаётся постоянной величиной, определяемой его размерами и конфигурацией. Эта величина называется электроёмкостью Q/j = С (12)

Измеряется электроёмкость в фарадах (1 Ф = 1 Кл/В). Для шара С=R/k.Имеется конфигурация, конструкция, для которых электроёмкость не меняется от наличия окружающих тел, и поле, создаваемые этими заряженными конструкциями в определённой части пространства, не меняется при перемещении окружающих тел. Такие конструкции называются конденсаторами. В качестве примера можно привести плоский конденсатор, представляющий собой две параллельные пластины размерами S каждая, расположенные на расстоянии d друг от друга. Его электроёмкость вычисляется по формуле

C=See_o/d, (13)

Е_д ~ 1/ r³ (7)

∮Е dS = g/e_o (8)

j = А/ q ₀ (9)

С = q/j (11) C = S C_i, 1/C = S 1/C_i

W = Uq/2 = CU²/2 = q²/2C (12)

.. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

Электрический ток. Сила тока. Единицы силы тока.

Электродвижущая сила, напряжение. Законы Ома.

Работа электрического тока.

Ток в различных средах.

Сопротивление проводников (резисторов). Зависимость сопротивления от температуры. Полупроводники.

Правила Кирхгофа для разветвлённой цепи.

I = U/R.

I = U/R.

R = rl/S

R = S R_i

1/R = S1/R_i

m = kIt

A = IUt

Q = I²Rt

P = IU

SI_i = 0

SI_i R_i = Se_i

Лекция 1б. МАГНЕТИЗМ

Магнитное поле и его характеристики.

Закон Ампера.

Сила Лоренца.

Магнитные свойства веществ.

Закон Био-Савара-Лапласа

B = F/Il.

F = ВIl sina

dB = (m₀BIdl sina)/4pr²

B = m₀I/2pr.

B= m₀I (sinb₁ + sinb₂)/4pd.

B = m₀Ir²/2(r² + d²)^3/2.

B = m₀I/2r.

F = qVB sina.

Ф = LI

W = LI²/2

1. Магнитное поле и его характеристики. Рассмотрим одно из проявлений электрического тока, которое рассматривалось на прошлой лекции – создание магнитного поля. Оно было обнаружено впервые в 1820 году Эрстедом. Во время эксперимента при замыкании электрической цепи магнитная стрелка, стоявшая рядом на подставке, среагировала, зафиксировав возникновение магнитного поля.

Постоянные магниты и их свойства, магнитное поле Земли были известны давно, но с этого времени (1820 г.) началось интенсивное изучение магнитного поля тока, исследование взаимосвязанных магнитных полей и электрических явлений. Проводники, по которым протекают токи, как мы уже упоминали, взаимодействуют, интенсивность и направление взаимодействия меняется с изменением силы тока и с изменением направления тока в одном из проводников. И это явление нельзя объяснить кулоновским взаимодействием, которое значительно слабее и иное проявление (если сопоставить рисунки, то в «б» они должны отталкиваться, а в «в» притягиваться).

а б в

Новое взаимодействие присуще только движущимся зарядам, т.е. току. Если между полюсами постоянного подковообразного магнита поместить проводник, по которому протекает ток, то он отклонится. Направление отклонения определяется направлением тока в проводнике и ориентацией полюсов постоянного магнита. Аналогичное взаимодействие можно пронаблюдать в поведении катушки с током в магнитном поле постоянного магнита и двух катушек с током.

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ

Электромагнитная индукция, Закон Фарадея. Закон Ленца

Самоиндукция. Индуктивность.

Электромагнитные колебания и волны. Принцип радиосвязи.

После опыта Эрстеда по обнаружению магнитного поля вокруг проводника с током, исследований магнитных взаимодействий токов и изучения взаимосвязанных магнитных и электрических явлений встал вопрос: если ток создает магнитное поле, то нельзя ли имея магнитное поле получить электрический ток, электрическое поле. Если опыт Эрстеда носил элемент случайности (исследования подошли к этому факту, но специально задача не ставилась), то теперь была поставлена перед учеными конкретная задача исследования.

После многочисленных экспериментов, проверки выдвинутых гипотез одному из большой группы ученых удалось зафиксировать электрический ток в замкнутом проводящем контуре при изменении потока магнитной индукции пронизывающего поверхность данного контура. Этот результат был получен английским ученым М. Фарадеем в 1831 году (спустя 11 лет после опыта Эрстеда). Это явление было названо явлением электромагнитной индукции, а возникающий ток - индукционным. Сейчас эти эксперименты Фарадея кажутся простыми, но чтобы первым прийти к этому результату, нужна была гениальная догадка и кропотливый труд – огромная серия опытов.

Пронаблюдаем один из этих опытов. Напомню, что поток магнитной индукции определяется формулой Ф=BS_n или при переменном В можем записать Ф = ∫ dФ = ∫ B_ndS.

Рассмотрим на данной установке замкнутый контур, пронизывающийся меняющимся магнитным потоком

e_инд.= -dФ/dt.

Z = Ö R² + (wL – 1/wC)².

N = I_эфU_эф cosj = I_мU_м cosj/2

T=2pÖ LC.

T = 2p/Ö 1/LC – (R/2a)².

Z = Ö R² + (Lw)²

tqj= Lw / R

∮ BS_n ∫Е dS∫

B = F/Il.

F = ВIl sina

dB = (m₀BIdl sina)/4pr²

B = m₀I/2pr.

B= m₀I (sinb₁ + sinb₂)/4pd.

B = m₀Ir²/2(r² + d²)^3/2.

B = m₀I/2r.

F = qVB sina.

Ф = LI

W = LI²/2

Дата добавления: 2014-01-06