Решение. Опыт состоит в выборке одного из имеющихся чисел. Построим множество исходов рассматриваемого опыта

U₁={выбрано натуральное число 60},

U₂={ выбрано натуральное число 61},

U₃={ выбрано натуральное число 62},

U₄={ выбрано натуральное число 63},

………………………………………………

………………………………………………

U₁₁={ выбрано натуральное число 70},

U₁₂={ выбрано натуральное число 71},

U₁₃={ выбрано натуральное число 72},

U₁₄={ выбрано натуральное число 73},

U₁₅={ выбрано натуральное число 74},

Таким образом, множество исходов рассматриваемого опыта состоит из пятнадцати элементов: U₁, U₂, U₃ ,…,U₁₃, U₁₄, U₁₅. Можно найти общее число исходов, не перечисляя их, для этого достаточно найти значение числового выражения 74-60+1. «Случайно выбранное натуральное число» означает равновозможность всех исходов данного опыта.

Поскольку, среди натуральных чисел от 60 до 74, лишь числа 60, 60+6=66, 66+6=72 кратны 6, то событию A - «выбранное число делится на 6» благоприятствуют 3 исхода. Поэтому, согласно классическому подходу к определению вероятности, искомая вероятность равна отношению числа исходов, благоприятствующих событию A, к числу всевозможных исходов, то есть .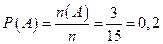

Ответ. 0,2.

4. Задание B10 (№ 320831) Агрофирма закупает куриные яйца в двух домашних хозяйствах. 55% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 5% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение: Пусть агрофирма закупила x куриных яиц у первого домашнего хозяйства и y куриных яиц – у второго, тогда среди купленных куриных яиц у первого и второго домашних хозяйств оказалось 0,55x и 0,05y яиц высшей категории соответственно. По условию задачи 35% куриных яиц агрофирмы – яйца высшей категории. Составим уравнение 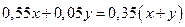. Полученное линейное уравнение двух переменных, к сожалению, не позволит найти значения переменных, в лучшем случае мы сможем с его помощью установить зависимость между переменными x и y. Поэтому обратимся к вопросу задачи, чтобы понять, что нужно знать для ответа на этот вопрос. Для нахождения вероятности события A - «купленное у агрофирмы куриное яйцо – яйцо из первого хозяйства» - нужно знать общее число куриных яиц у агрофирмы, в нашем случае – (x+y), а также число куриных яиц, закупленных у первого домашнего хозяйства, в нашем случае - x. Таким образом, в соответствии с классическим подходом к определению вероятности, ответом на вопрос задачи будет значение выражения 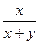. Из уравнения 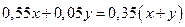следует, что . Подставляя в выражение 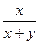вместо переменной y выражение 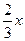, получаем 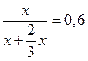. Итак, искомая вероятность равна 0,6.

Дата добавления: 2014-01-06