
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дискретные случайные величины
|
|
|
|
Пусть 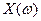 -- дискретная случайная величина на вероятностном пространстве, принимающая значения
-- дискретная случайная величина на вероятностном пространстве, принимающая значения 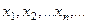 . Тогда для каждого
. Тогда для каждого 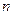 определена вероятность
определена вероятность
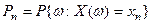 где
где 
т.е. СВ принимает заданное значение 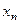 с вероятностью
с вероятностью  . Для того, чтобы найти
. Для того, чтобы найти  , нужно в
, нужно в 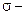 алгебре
алгебре 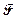 выбрать все исходы эксперимента, в результате которых СВ приняла значение
выбрать все исходы эксперимента, в результате которых СВ приняла значение 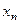 и объединить их в событие. Вероятность этого события и есть вероятность того, что случайная величина приняла значение
и объединить их в событие. Вероятность этого события и есть вероятность того, что случайная величина приняла значение 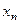 .
.
Пример. Стохастический эксперимент-бросание двух игральных костей. Случайная величина – сумма выпавших очков на двух костях. Найти вероятность того, что выпадет 6 очков.
Пространство элементарных событий 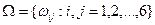 . Вероятность одного исхода (элементарного события) равна
. Вероятность одного исхода (элементарного события) равна  . Объединим в событие исходы, при которых выпадает суммарное число очков, равное 6:
. Объединим в событие исходы, при которых выпадает суммарное число очков, равное 6:
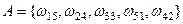 . Тогда
. Тогда 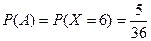 .
.
Для дискретной случайной величины закон распределения полностью определяется указанием ее значений 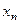 (
( ) и вероятностей
) и вероятностей 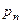 (
( ), с которыми случайная величина принимает эти значения.
), с которыми случайная величина принимает эти значения.
Ряд распределения СВ – таблица, в которой для каждого значения случайной величины указана вероятность его появления. В случае конечного пространства 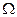 ряд распределения имеет вид
ряд распределения имеет вид
Значения случайной
величины 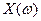
|

|
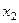
| … |

|
Вероятности 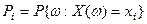
| 
| 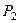 
| … | 
|
где  . и
. и  .
.
В случае счетного пространства 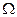 ряд распределения может быть представлен таблицей
ряд распределения может быть представлен таблицей
Значения случайной
величины 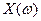
|

|
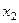
| … |

| … |
Вероятности 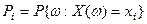
| 
| 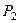
| … | 
| … |
где  . и
. и 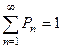 .
.
Ряд из вероятностей должен сходиться и иметь сумму, равную единице. В силу необходимого признака сходимости числового ряда 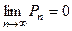 . Поэтому ряд распределения можно оборвать на некотором значении n.
. Поэтому ряд распределения можно оборвать на некотором значении n.
Графическое изображение ряда распределения называется многоугольником распределения.
Пример. Игрок подбрасывает монету 2 раза. Если выпадает герб, то он получает 1 рубль, если выпадает решетка, то ничего не получает. Случайная величина 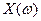 – выигрыш игрока. Построить ряд распределения, многоугольник распределения, функцию распределения и ее график.
– выигрыш игрока. Построить ряд распределения, многоугольник распределения, функцию распределения и ее график.
Пространство элементарных событий  . Определим события, в результате наступления которых выигрыш игрока равен нулю, единице и двум.
. Определим события, в результате наступления которых выигрыш игрока равен нулю, единице и двум.
 ,
,  ,
, 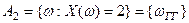 . Вероятности этих событий равны соответственно
. Вероятности этих событий равны соответственно 
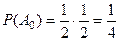 ,
, 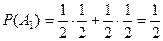 ,
, 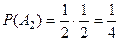 .
.
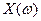
| |||
| P | 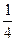
| 
| 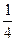
|
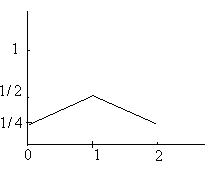
Здесь приведен ряд распределения и многоугольник распределения.
Функция распределения дискретной случайной величины разрывна. Ее график – ступенчатая линия, имеющая разрывы при тех значениях случайной величины, вероятность которых отлична от нуля. Величина скачка в точке разрыва равна вероятности соответствующего значения случайной величины. Для построения графика функции распределения дискретной случайной величины нужно построить таблицу накопленных вероятностей для данной случайной величины и по этой таблице построить соответствующую ступенчатую линию. В данном случае функция распределения случайной величины имеет вид
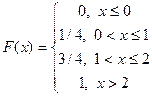

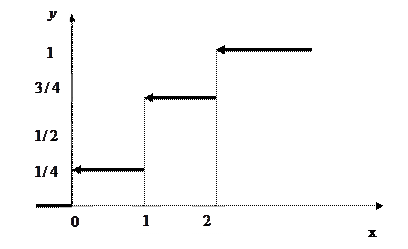
На рис. представлен график функции распределения
. Примеры дискретных случайных величин.
Биномиальное распределение. Схема Бернулли.
Пусть производятся независимые испытания и при каждом испытании может быть 2 исхода: успех с вероятностью  или неудача с вероятностью
или неудача с вероятностью  , при этом (
, при этом (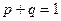 ).
).
Примеры
1) Стрельба по цели. При каждом выстреле 2 исхода: попадание или промах.
2) Проверка наугад выбранного изделия, которое может оказаться качественным или бракованным.
3) Подбрасывание симметричной монеты.Может выпасть герб или решетка.
Построим вероятностную модель эксперимента в случае  .
.
Пространство элементарных событий 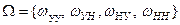 .
.
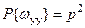 ,
, 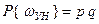 ,
, 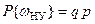 ,
, 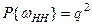 . Поскольку испытания независимы, то вероятности элементарных исходов определяются как произведение вероятностей.
. Поскольку испытания независимы, то вероятности элементарных исходов определяются как произведение вероятностей.
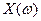
| |||
| P | 
| 
| 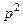
|
В качестве случайной величины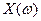 рассмотрим число успехов в серии из 2 испытаний. Построим ряд распределения случайной величины
рассмотрим число успехов в серии из 2 испытаний. Построим ряд распределения случайной величины
При этом 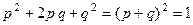 , так как
, так как  .
.
Пусть теперь опыт повторяется 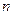 раз. При каждом опыте событие А (успех) происходит с вероятностью
раз. При каждом опыте событие А (успех) происходит с вероятностью  и не происходит с вероятностью
и не происходит с вероятностью 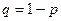 , причем эти вероятности от опыта к опыту не меняются. Случайная величина
, причем эти вероятности от опыта к опыту не меняются. Случайная величина 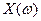 – число успехов в серии из
– число успехов в серии из 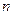 испытаний, Найдем вероятность того, что
испытаний, Найдем вероятность того, что 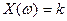 , т.е. что событие А (успех) наступит
, т.е. что событие А (успех) наступит 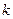 раз (а, следовательно, неуспех наступит
раз (а, следовательно, неуспех наступит  раз).Найдем вначале, что событие А (успех) произойдет при первых
раз).Найдем вначале, что событие А (успех) произойдет при первых 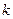 опытах и не произойдет при последних
опытах и не произойдет при последних опытах. Применяя теорему умножения вероятностей, получим
опытах. Применяя теорему умножения вероятностей, получим 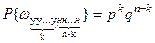 . Но событие А может произойти
. Но событие А может произойти 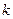 раз и в другой последовательности. Общее число всех возможных последовательностей равно
раз и в другой последовательности. Общее число всех возможных последовательностей равно  . Вероятность появления события А для каждой такой последовательности равна
. Вероятность появления события А для каждой такой последовательности равна  . Вероятность появления какой либо одной из этих последовательностей найдем с помощью теоремы сложения вероятностей
. Вероятность появления какой либо одной из этих последовательностей найдем с помощью теоремы сложения вероятностей
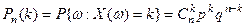 , где
, где  .
.
Полученная формула является формулой для 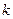 –го члена бинома Ньютона
–го члена бинома Ньютона  . Поэтому такое распределение вероятностей называется биномиальным. Впервые это распределение подробно изучил Бернулли. Поэтому стохастический эксперимент, приводящий к биномиальному распределению, называется схемой Бернулли.
. Поэтому такое распределение вероятностей называется биномиальным. Впервые это распределение подробно изучил Бернулли. Поэтому стохастический эксперимент, приводящий к биномиальному распределению, называется схемой Бернулли.
Функция распределения биномиального закона имеет вид
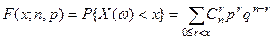 ,
,
где  неотрицательное целое число.
неотрицательное целое число.
Пример. Прибор состоит из четырех элементов. Вероятность отказа каждого из них равна  . Найти вероятность отказа 0,1,2,3,4 элементов во время работы прибора.
. Найти вероятность отказа 0,1,2,3,4 элементов во время работы прибора.



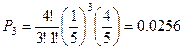

Сумма всех вероятностей равна 1, так как эта сумма есть вероятность достоверного события.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 745; Нарушение авторских прав?; Мы поможем в написании вашей работы!