Непрерывные распределения

Лекция 5.

Напомним, что непрерывной случайной величиной называется такая, множеством значений которой является интервал или вся числовая ось. Для непрерывной случайной величины 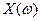существует такая интегрируемая функция 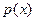, что для 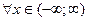функция распределения вероятностей имеет вид

(1)

Функция , где , называется плотностью вероятности случайной величины или плотностью распределения.

Свойства плотности распределения.

1. Если 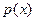– непрерывная функция в промежутке , то 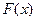– дифференцируемая функция и

(2)

как производная от интеграла по верхнему пределу.

2. Плотность вероятности является неотрицательной функцией

,

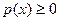так как функция 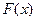является неубывающей функциейи следовательно .

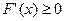3. .

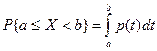Это равенство следует из соотношений

.

Эта величина численно равна площади криволинейной трапеции, ограниченной графиком функции , осью 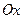и прямыми и 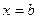. Отсюда также следует, что вероятность того, что непрерывная случайная величина примет заданное значение, равна нулю:.

4. Если 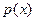– непрерывная функция, то

,

так как .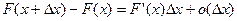

Величина 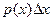называется элементом вероятности и представляет собой вероятность того, что случайная величина примет значения, заключенные в промежутке между 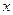и .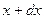

5. . Это равенство представляет собой условие нормировки для плотности вероятности и следует из равенства 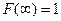, поскольку . Геометрически условие нормировки плотности вероятности означает, что площадь области, ограниченной графиком плотности распределения и осью абсцисс, равна единице. Она равна вероятности того, что случайная величина примет значения между и 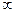, т.е. вероятности достоверного события.

Примеры непрерывных распределений.

1. Равномерное распределение на отрезке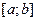

На отрезок 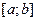числовой прямой наугад бросают точку, причем считают все положения точки равновозможными. Тогда . Пусть 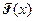– – 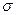алгебра измеримых множеств из 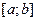и 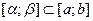. Тогда .

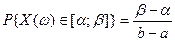При каждом 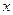, т.е. 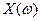– случайная величина. Функция распределения этой случайной величины имеет вид

Плотность вероятности равномерного распределения равна

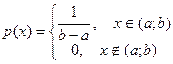
Ниже приведены графики функции распределения и плотности вероятности для равномерного распределения случайной величины

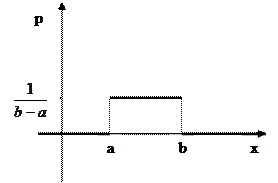
Равномерное распределение используется при генерировании на ЭВМ случайных чисел.

Дата добавления: 2014-01-06