Алгоритм решения задачи 3

Будем постепенно приписывать всем вершинам графа индексы μ _к ≥ 0:

1. Вершине А припишем индекс 0, всем остальным вершинам индекс + ∞.

Замечание. В реальных задачах в роли + ∞ выступает любое выбранное пользователем число, намного превосходящее сумму всех весов λ _к графа_.

2. Перебираем последовательно все пары смежных вершин x и y

μ _x λ _xy μ _y

• •

x y

	μ y > μ x + λ xy

Каждый раз проверяем неравенство

Если оно выполнено, то уменьшим индекс μ _y, заменив его на μ _x + λ _xy.

3. Процесс останавливаем, когда ни один индекс уже нельзя уменьшить. В этот момент вершина В имеет некоторый индекс μ _В - это и есть наименьшая сумма весов.

Построим путь с такой суммой.

4. Среди вершин смежных с В обязательно найдется вершина С, для которой выполняется точное равенство μ_В= μ_С+ λ_СВ

Возвращаемся в С и повторяем процесс.

Т.к. индексы все время уменьшаются, рано или поздно придем в вершину индекса в 0, т.е. вершину А.

Один или несколько путей построены.

§ 3. Представление графов в памяти компьютера.

I. Матрица смежности

Матрица – любая прямоугольная таблица чисел.

	…   …   …

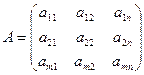
Размер m x n – m – строк,- столбцов

a _ij - номер элемента I – строка, - столбец

Если m = n то матрицу называют квадратной n-го порядка

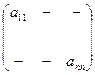
Квадратная матрица называется симметричной, если ее элементы симметричны относительно главной диагонали, т.е. a_ji = a _ij.

Дата добавления: 2014-01-06