Код Прюфера

Пример

0 1

00 01 11

010 110 111

Определение. Множество двоичных строк соответствующих висячим вершинам называют префиксным кодом бинарного ордерева.

Для приведенного примера префиксный код таков: { 00, 010, 110,111 }

Префиксный код определяет ордерево однозначно.

Пример. Восстановить ордерево по префиксному коду

{ 000, 0010, 0011, 01, 100, 1, 010, 11 }

Из кода видно, что дерево имеет четыре уровня.

1 0 1

2 00 01 10 11

000 001 100 101

4 0010 0011 1010

Для небинарных деревьев возможно использование троичной системы и т.д., но это плохо совместимо с памятью компьютера.

Другой подход к кодированию деревьев это так называемый

Рассмотрим дерево (или ордерево) с n – произвольно пронумерованными вершинами. Действуем по циклическому алгоритму из n-2 шагов: в списке 1,2,3,…,n слева направо ищем первую висячую вершину. Пусть это а_к, ищем с какой вершиной она смежна, пусть это b_к, тогда вершину b_к заносим в новый список будущий код Прюфера, а вершину а_к удаляем и из дерева, и из списка. В конце получим список { b₁,b₂,…,b_n-2 }- код Прюфера

Пример: Построить код Прюфера для дерева

·

· ·

· ·

3 5 6

· · ·

Во-первых, n =8 Þ n-2=6 – в коде Прюфера будет 6 чисел.

Идя по списку всех вершин

1, 2, 3,4,5,6,7,8

по алгоритму строим код Прюфера:

{7,4,4,4,2,2}

Теорема. Код Прюфера однозначно определяет дерево, ордерево вместе с нумерацией вершин.

Пример: Восстановить ордерево по коду Прюфера {2,3,5,6,8,6,3}

Видим сразу, что n–2 =7 Þ n=9, в ордереве будет 9 вершин

Идя по списку всех вершин

1, 2, 3,4,5,6,7,8,9

и используя понятие неприкосновенной вершины, мы восстанавливаем дерево.

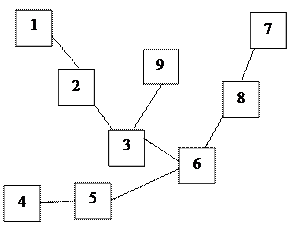
Легко проверить, что у построенного дерева именно такой код Прюфера,

как заданный в условии.

Замечание. Код Прюфера является оптимальным по объему памяти способом кодирования деревьев (любых, а не бинарных).

Дата добавления: 2014-01-06