Основные теоретические сведения элементов векторного анализа

Классическая электродинамика основана на представлении о непрерывном электрическом заряде и сплошной (непрерывной) покоящейся среде. В среду вводится покоящаяся ортогональная система координат, в которой определена покоящаяся точка наблюдения 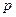. В частности, в декартовой системе координат (ДСК) 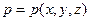. В математическом смысле непрерывные функции координат 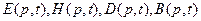описывают реально существующее физическое поле в каждой точке .

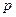Для описания физических полей принято использовать их математические модели – скалярные и векторные поля. В произвольной системе координат 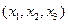скалярное поле φ приобретает вид некоторой функции φ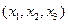, принимающей численные значения – действительные или комплексные. Векторное поле А задается тремя проекциями на единичные векторы (орты) выбранной системы координат:

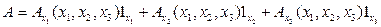(3)

Для характеристики величины и направления скорости изменения скалярного поля в пространстве вводят градиент этого поля:

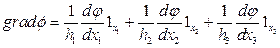(4)

где 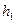, 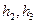- коэффициенты Лямэ по координатам 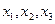, являющиеся коэффициентами пропорциональности между дифференциалами обобщенных координат и бесконечно малыми ребрами элементарного параллелепипеда в выбранной точке пространства.

Значения коэффициентов Лямэ для наиболее употребительных координатных систем:

декартова система координат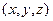

;

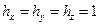цилиндрическая система координат )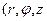

;

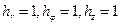сферическая система координат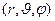

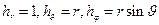
Конкретно градиент вычисляют следующим образом:

в декартовой системе координат

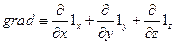(5)

в цилиндрической системе координат

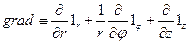(6)

в сферической системе координат

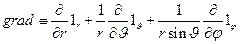(7)

Описание дифференциальных свойств векторного поля несколько сложнее. Векторное поле A принято характеризовать скалярным полем – дивергенцией div A и векторным полем – ротором rot A. Значение дивергенции равно плотности источников рассматриваемого поля в заданной точке пространства. Трактовка ротора векторного поля сложнее; можно считать, что оно в известном смысле характеризует степень отличия исследуемого поля от однородного.

Дивергенцию векторного поля A вычисляют путем дифференцирования его проекций по определенным правилам:

в декартовой системе координат

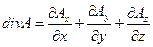(8)

в цилиндрической системе координат

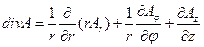(9)

в сферической системе координат

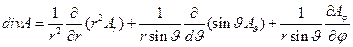(10)

В произвольной ортогональной криволинейной системе координат

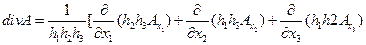(11)

Проекции ротора векторного поля имею вид:

в декартовой системе координат

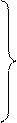
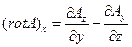
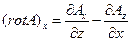(12)

в цилиндрической системе координат

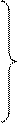
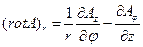
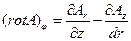(13)

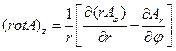
в сферической системе координат

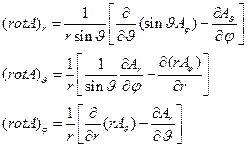(14)

Ротор векторного поля A в произвольной системе координат выражают через проекции исходного поля и коэффициенты Лямэ:

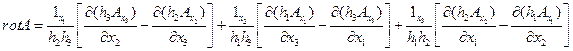(15)

Дифференциальные операции со скалярными и векторными полями удобно записывать с помощью оператора Гамильтона 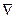. По определению

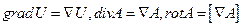(16)

В декартовой системе координат оператора Гамильтона есть символический вектор

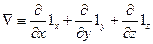(17)

Из дифференциальных векторных операций второго порядка широкое применение в электродинамике находит оператор 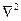, закон действия которого на векторное поле A описывается соотношением

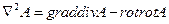(18)

Дифференциальная операция второго порядка, действующая на скалярное поле, задается оператором Лапласа

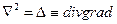
Оператор Лапласа в различных координатных системах записывается следующим образом:

в декартовой системе координат

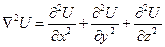(19)

в цилиндрической системе координат

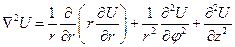(20)

в сферической системе координат

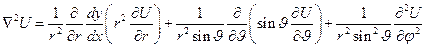(21)

Для графического изображения векторных полей принято строить картину их силовых линий.

Дата добавления: 2014-01-06