Лекция 2. Правильность и статистическая обработка результатов анализа

Правильность и статистическая обработка результатов анализа

План:

Правильность анализа

Характеристика погрешностей

Статобработка результатов анализа

1. Задача количественного химического анализа найти содержание отдельных элементов в анализируемом материале. Главное требование к анализу - полученные результаты должны отражать истинное содержание элементов в пробе. Любое аналитическое определение состоит из следующих этапов:

1) отбор пробы;

проведение анализа;

статобработка результатов анализа.

Проба материала, поступающая в лабораторию должна быть представительной, т.е. состав пробы и всей партии обьекта анализа должны быть идентичными.

2. Необходимым этапом физико-химических методов является оценка возпроизводимости и правильности анализа. Погрешности бывают грубыми, систематическими и случайными.

Грубые ошибки: а) ошибка аналитика (неправильный отбор аликвоты), б) выход из строя измерительных приборов.

Систематические ошибки - это односторонние погрешности, вызванные неисправностью измерительного прибора, недостатком метода.

Случайные ошибки не имеют видимой причины. Оценка случайных погрешностей проводится на основе теории математической статистики. Для характеристики качества анализа рекомендуется использовать определяемые понятия правильность и воспроизводимость, под которыми надо понимать термин точность. Воспроизводимость представляет собой необходимый, но недостаточный признак правильности результатов. Без удовлетворительной возпроизводимости нет и точности. Однако даже хорошая воспроизводимость вовсе не доказывает точность метода.

Правильность анализа (ПА) характеризуется расхождением между средним и истинным результатом. ПА нельзя установить посредством статистской обработки результатов. Надо применять другие, экспериментальные методы проверки правильности. К ним относят следующие методы:

А) Проведение анализа двумя или несколькими независимыми методами. Применение стандартных образцов (СО). СО- это эталоны химического состава материалов. Каждый СО снабжен официальным документом - паспортом, в которой указано аттестованное содержание отдельных элементов. Чтобы установить правильность анализа какого-либо материала, из имеющегося в лаборатории набора СО выбирают тот, который по своему составу в наибольшей степени приближается к предполагаемому составу анализируемой пробы. Затем проводят параллельный анализ пробы и стандартного образца, устанавливая содержание отдельных элементов в них. Считается, что использованный метод анализа дает правильные результаты, если найденное содержание отдельных элементов в стандартном образце соответствует паспортным данным, установленным при аттестации этого образца.

B) Метод добавок. Ведут несколько параллельных определений, прибавляя к некоторым пробам точно известные количества определяемого элемента. При правильном анализе количество элемента, найденное в пробах с добавками и без них, должно соответствовать количеству добавки. Например, определяя железо в растворе нашли, что проба без добавки содержала 0,2378 г Ғе203, а проба с добавкой 0,1000 г Ғе2О3 - 0,3375 г Ғе2Оэ. Разность 0,0997г = 0,1000 г.. Разность 0,0997г = 0,1000 г. Анализ можно считать правильным.

При полном анализе, какого либо материала сумма всех компонентов должна быть равной 100% или незначительно отличаться от этого значения.

Применяя эти методы, можно говорить о правильности анализа. Тем не менее, систематические погрешности все же возможны. Важно, чтобы они не выходили за некоторые пределы.

Рассмотрим зависимость результатов определения от наличия систематических погрешностей.

В одних случаях результат может отличаться от истинного всегда на одно и тоже значение, т. е. погрешность будет постоянной независимо от размера навески.

В других случаях систематическая погрешность влияет на результаты анализа иначе. Увеличение навески анализируемого материала влечет за собой возрастание только абсолютной погрешности, однако относительная погрешность остается при этом одной и той же. Пример: иодометрическое определение меди в сплавах с примесями железа.

2Сu2+ + 4I- =2СuI + I2

Затем I2 +2 Nа2S203 = 2NаI + Nа2S406 и по расходу тиосульфата вычисляют соединение Си 2+. Однако Ғе3+ с иодид-ионами I- дают I2:

2 Ғе3+ +2I- = 2Ғе2++I2

Поэтому в присутствии Ғе3+получаются повышенные результаты для Си2+, причем абсолютная погрешность возрастает с увеличением размера навески. Однако относительная погрешность не зависит от количества взятого для анализа материала. Предположим, что навеске 0,1г отвечает + погрешность 0,2 мг, тогда при навеске 0,2 г, она увеличивается до 0,4мг, однако в обоих случаях относительная погрешность остается неизменной и составит:

3. Статистическая обработка (СТО) результатов анализа имеет две основные задачи:

представить результаты многих определений в компактной форме.

оценить надежность полученных результатов, т.е. степень их соответствия истинному определяемого элемента в образце.

Среднее значение полученного результата по разным причинам может отличаться от истинного. Разница между ними определяет правильность определения и представляет собой систематическую погрешность, которая повторяется от опыта к опыту. Причиной случайной погрешности могут быть несовершенство приборов, влияние посторонних компонентов, загрязнение реактивов и т.д. Например, при фотометрическом определении Си2+ получены десять значений оптической плотности D:

Таблица 2.1

Математическая обработка результатов анализа

Полученные расхождения можно объяснить случайными погрешностями. Однако, если в результате неправильно нанесенной шкалы ФЭК постоянно получают завышенные показатели D, это будет причиной систематической ошибки, повторяющейся от опыта к опыту.

Рассмотрим обработку данных. Сначала выводим среднее арифметическое

Х = 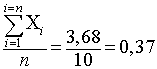(2.1)

Отклонения dі характеризуют погрешность определения. По значениям di вычисляем дисперсию S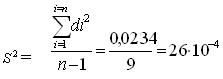2.

(2.2)

S = называют стандартным отклонением: (2.3)

S =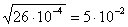

Известна еще одна величина – точность прямого измерения (ε), которую определяют по известному уравнению. При использовании этого уравнения задаются значением надежности (α), т.е. долей случаев в которых при данном числе измерений среднем арифметическом лежит в определенных пределах. При физико-химических измерениях обычно принимают α = 0,95 или α = 0,99. Это означает, что 95 или 99% всех измерений лежит в указанных пределах:

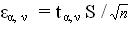(2.4)

Коэффициент t α,ν называют критерием Стъюдента. ν = n-1 и его называют числом степеней свободы.Величину t α,ν находят по специальным таблицам в зависимости от α и ν = n - 1. Их значения приведены в таблице 2.

Таблица 2.2

Коэффиценты Стьюдента t α,ν

Исходя из таблицы № 1:

ν = 10-1= 9; = 10 = 3,2

t 0.95 = 2,26

Это большая погрешность в таблице 1 разброс составляет от 0,27 до 0,47. Видимо здесь имеют место какие-то грубые погрешности. Такие грубые погрешности можно определить при помощи трех критериев:

по стандартному отклонению d груб >3S/ (2.5)

по точности прямого измерения (2.6)

по Q - критерию, которую вычисляют по формуле: 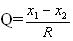(2.7)

R - размах варьирования (разность между предельными значениями измеряемой величины) Значения Q-критерия приведены в таблице 3.

Таблица 2.3 Значения Q-критерия

Применяя эти три критерия, получаем:

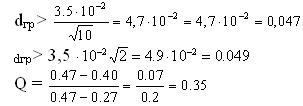
По первым двум критериям первое и десятое измерения должны быть исключены как грубые погрешности.

А по Q - критерию необходимость исключения ставится под сомнение, так как значение Q меньше табличного. Поэтому рекомендуют проверить такие значения по одному из первых критериев.

Теперь делаем вторичную обработку (исходя из табл. 2, данные заносим в табл. 1)

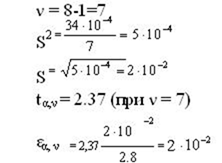
Следовательно, D= 0.37 ұ 0.02 (Dср = 0.37)

После исключения грубых погрешностей точность измерений значительно повышается.

Т.о. стандартное отклонение S, а также точность прямого измерения S характеризуют точность результатов наблюдения

Дата добавления: 2014-01-06