Механические колебания

Общие сведения о колебаниях

КОЛЕБАНИЯ И ВОЛНЫ

Лекция 8	Малые колебания. Гармонический и ангармонический осциллятор. Уравнение гармонических колебаний.
	Пружинный, физический и математический маятники.

Колебаниями называют периодические движения, совершаемые системой относительно некоторого среднего значения. В зависимости от физической природы повторяющихся процессов различают механические колебания - колебания маятников, струн и т.д., электромагнитные колебания - колебания напряженностей электрических и магнитных полей в колебательном контуре и другие виды колебаний. Колебания различной природы подчиняются одинаковым закономерностям. Колебания лежат в основе многих физический явлении и технических процессов. В зависимости от характера воздействия на систему различают собственные (незатухающие) колебания, свободные, вынужденные и др. Простейшими являются гармонические колебания, т.е. такие, при которых колеблющаяся величина изменяется по закону синуса или косинуса. Их и будем рассматривать в дальнейшем.

Наиболее простым видом гармонических колебаний являются колебания математического маятника (Рис. 25.1) - колебания материальной точки, подвешенной на невесомой нити. Если вывести тело из состояния равновесия, то возникает результирующая сила 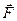,стремящаяся вернуть тело к прежнему положению. Запишем уравнение его движения. Т.к. сила 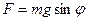направлена противоположно смещению маятника x, то:

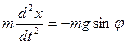(25.1)

Для малых углов отклонения 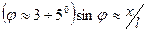и вместо (25.1) получим:

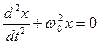(25.2)

где

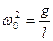(25.3)

Величина 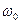называется круговой или циклической частотой. Другой случай возникновения гармонических колебаний -колебания пружинного маятника (Рис. 25.2). Если вывести груз из положения равновесия, то со стороны пружины на него будет действовать возвращающая сила упругости F=-kx, где k- жесткость. Тогда или 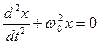(25.4) где в этом случае 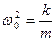(25.5)

Еще одним видом гармонических колебаний является колебание физического маятника - колебания тяжелого тела, колеблющегося вокруг оси, не проходящей через центр тяжести (Рис.25.3). Если центр тяжести расположен на расстоянии l от оси вращения в т.А, то момент силы тяжести равен:

M=mglsinφ

Этот момент заставляет отклоненный маятник вернуться в исходное состояние, поэтому уравнение его движения будет:

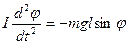(25.6)

где I - момент инерции маятника относительно оси вращения. Для малых отклонений 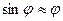. Получим:

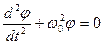(25.7) 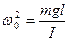(25.8)

Как видно, во всех случаях гармонические колебания описываются уравнением одного вида (25.2), (25.4), (25.7). Решением такого уравнения является функция:

(25.9)

A=x_max называют амплитудой колебания, - фазой колебания, φ₀ - начальная фаза.

Амплитуда и начальная фаза определяются начальными условиями - значениями смещения и скорости при t=0:x=x₀, V=V₀, где 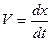- скорость колебаний.

Т.к. гармонические колебания представляют периодический процесс о периодом Т, а период косинуса равен 2π, то из (25.9) находим:

, откуда:

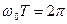или 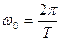(25.10)

С учетом этого из (25.3), (25.5), (25.8) находим периоды рассмотренных колебаний:

для математического маятника -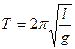

пружинного -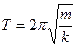

физического -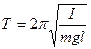

Дата добавления: 2014-01-06