КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Лапласа
|
|
|
|
Поверхность жидкости представляет собой как бы натянутую резиновую пленку, которая благодаря силам поверхностного натяжения стремится сократиться. Поэтому под ее искривленной поверхностью возникает добавочное давление, точно так же, как внутри резинового шара или мыльного пузыря давление на определенную величину больше давления наружного воздуха.
Для вычисления этого давления рассмотрим шарообразную каплю жидкости радиуса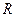 
. Для изменения объема капли на 
необходимо затратить работу 
, которая идет на изменение поверхностной энергии 
. Таким образом,
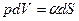(12.5)
Так как для шара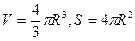 
, то:
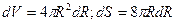
Подставляя это в (12.5), получим:
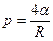(12.6)
Это выражение называют формулой Лапласа, которая определяет избыточное (капиллярное) давление - положительное под выпуклой поверхностью и отрицательнее - под вогнутой.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 352; Нарушение авторских прав?; Мы поможем в написании вашей работы!