Вывод основного уравнения упругого режима

Приток к скважине в пласте неограниченных размеров

Считаем пласт упругим, горизонтальным и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным к точечному стоку (эксплуатационная скважина) или от точечного источника (нагнетательная скважина).

Рассмотрим процесс перераспределения давления при неустановившимся плоском радиальном движении жидкости. Для этого запишем уравнение пьезопроводности в цилиндрической системе координат

. 5.12

Предположим, что возмущение вызвано мгновенным стоком, существовавшим в момент t=t^/. Для этого случая решение уравнения (5.12) имеет вид

, 5.13

где А и С - некоторые постоянные.

Найдём значения постоянных. Для этого будем считать, что в момент времени t=t^/ давление в пласте было р=р_к=const. Тогда при r>0 и при t=t^/ второй член правой части обращается в неопределённость типа ¥/¥ и определяется по правилу Лапиталя, что даёт С=р_к Таким образом,

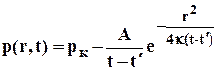, 5.14

Для определения коэффициента А воспользуемся соотношением (5.4) для определения объёма высвобождающейся жидкости для случая кольцевого элемента пласта с внутренним радиусом r, толщиной h и шириной dr, а также учтем падение давления Dр=p₀-p по (5.14)

dt_з=b^*Dрdt₀ =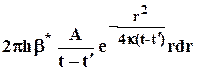. 5.15

.

После интегрирования (5.15) в пределах от 0 до ¥ получим объём жидкости t₂, выделившейся из всего пласта и, следовательно, определим коэффициент А

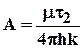. 5.16

Т.о. в случае скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно, изменение давления во времени определяется соотношением

, 5.17

Если скважина была введена в некоторый момент времени и действовала непрерывно с постоянным дебитом Q=Q₀ в течении времени dt^/, то за этот промежуток времени через сток выделяется из пласта объём dt₂=Qdt^/ и, следовательно, из (5.17) следует

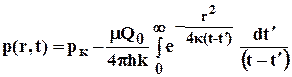, 5.18

Интеграл правой части носит название интегрально-показательной функции

и с учетом данного обозначения решение для изменения давления запишется в виде

, 5.19

Формула (5.19) является основной формулой теории упругого режима пласта.

Интегрально-показательная функция имеет вид (рис.5.1) и обладает следующими свойствами:

* - Ei(-u) изменяется от 0 до ¥ при изменении аргумента от 0 до ¥;

* функция - Ei(-u) представляется в виде сходящегося ряда

5.20

Для малых значений u <1 можно принять

5.21

Так погрешность применения (5.21) не превышает 0,25% при u <0,01; 5,7% - при u <0,1

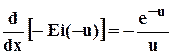. 5.22

С учетом соотношения (5.21) основное уравнение (5.19 перепишется в виде

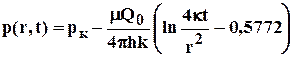, 5.23

Полученную зависимость можно использовать при числе Фурье 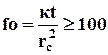с погрешностью не превышающей 0,6%. Практически это означает, чтоуже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (5.23), будут иметь погрешность не превышающую 0,6%. Формулу (5.23) можно использовать и для расчета падения давления в конечном пласте, а именно, погрешность расчета давления при этом не превышает 1%, если r_к >1000r_c и fo <3,5^.10⁵ или Fo <0,35.

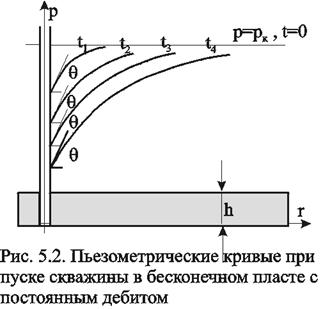
Рассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса r_c c постоянным дебитом Q₀ (рис.5.2). Для точек вблизи забоя можно пользоваться формулой (5.23): дифференцируя её по координате r, найдём градиент давления

.

Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r²<<0,03^.4kt, практически не завист от времени и определяется по той же формуле, что для установившейся плоскорадиальной фильтрации несжимаемой жидкости. Для указанных значений r пьезометрические кривые представляют собой логарифмические линии (рис.5.2). Углы наклона касательных на забое скважины одинаковы для всех кривых.

Дата добавления: 2014-01-06