Потенциальный барьер на границе металл-вакуум

В предыдущем параграфе мы уже указывали, что электрон проводимости в металле находится в потенциальной яме (см. рис. 1.1). В данном разделе нам необходимо детально выяснить, как описывается потенциальный барьер для электрона вблизи границы металла, для того, чтобы выяснить механизм выхода или механизм эмиссии электронов.

Будем рассматривать следующую модель, представленную на рис. 2.1. Образец металла ориентирован таким образом, что электрон двигается вдоль оси х через границу металл-вакуум, которая компланарна плоскости yz. В квантовой механике известна задача об отражении частицы от прямоугольного полубесконечного потенциального барьера, показанного на рис. 2.2. Решение данной задачи дает следующий результат. В области I, идентифицируемой в нашем случае с объемом металла, волновая функция электрона имеет осциллирующий вид, в области II, за пределами металла, экспоненциально затухает

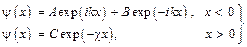. (2.1)

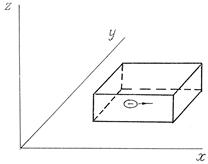
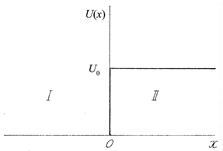
Рис. 2.1

Рис. 2.2

Из этого результата можно сделать вывод, полезный для дальнейшего рассмотрения: над поверхностью металла имеет место как бы “пар” из электронов, т.е. электроны проникают под барьер. На поверхности металла существует двойной электрический слой, обусловленный, с одной стороны, положительным зарядом ионов, возникшем из-за дефицита электронов в приповерхностной области со стороны металла, и, с другой стороны, отрицательным зарядом электронного “пара”. Толщина этого слоя очень мала, порядка длины волны электрона, что составляет единицы ангстрем.

В электростатике существует метод изображений (см. рис. 2.3). Суть его, применительно к нашему случаю, заключается в следующем. Если на расстоянии х справа от поверхности металла находится электрон, то слева на том же расстоянии от границы, в глубине металла, индуцируется “дырка” с эффективным положительным зарядом, равным по модулю заряду электрона. “Дырка” образуется благодаря перераспределению в металле, а точнее, на его поверхности, электронов проводимости на фоне положительно заряженных ионов. Сила электростатического взаимодействия между электроном и “дыркой”, очевидно, равна

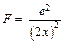. (2.2)

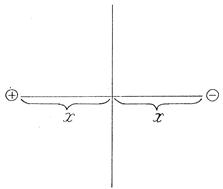
Рис. 2.3

Таким образом, для того, чтобы покинуть металл, электрону необходимо преодолеть два препятствия: пересечь двойной слой, препятствующий его выходу, и совершить работу против сил изображения. Бардин детально исследовал задачу о поведении электрона, покидающего металл, и показал, что на расстоянии от поверхности, превышающем постоянную решетки, можно пользоваться представлениями о силах изображения. Шоттки предложил на расстояниях от поверхности, меньших постоянной решетки a, считать силу изображения постоянной и равной при х = а, т.е.

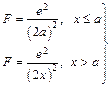. (2.3)

Используя (2.3), мы можем подсчитать работу, которую необходимо затратить для того, чтобы переместить электрон из металла на бесконечно удаленное расстояние, т.е. в свободное состояние

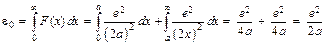. (2.4)

Величина e₀ называется полной работой выхода. Текущая работа или потенциальная энергия электрона по отношению к его состоянию в металле равна

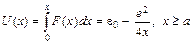. (2.5)

Формулу (2.5) полезно проиллюстрировать диаграммой процесса эмиссии, представленной на рис. 2.4. Нулевой уровень энергии соответствует дну зоны проводимости. Слева изображена функция распределения электронов проводимости по энергиям в системе координат, повернутой на девяносто градусов. Из рис. 2.4 ясно, что покидать металл могут лишь электроны высокоэнергетического “хвоста” функции распределения, у которых энергия e > e₀. Такой вид эмиссии носит название “термоэлектронная эмиссия”. Физический механизм термоэмиссии  испарение электронов.

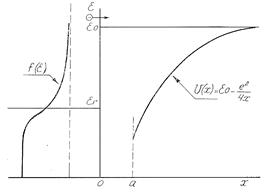
Рис. 2.4

Рассмотрим теперь более сложный случай. Пусть имеет место электрическое поле с напряженностью Е, тянущие электроны из металла. Формулы (2.3) и (2.5) перепишутся следующим образом

(2.6)

и

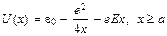. (2.7)

При записи (2.6) необходимо учесть, что за положительное направление силы считается направление справа налево, т.е. к металлу. Диаграмма процесса эмиссии в данном случае будет выглядеть следующим образом (см. рис. 2.5). Барьер на границе металл-вакуум будет теперь конечной ширины с максимумом при координате х = х_m и энергии e = e _m. Из квантовой механики известно, что через барьер конечной ширины частицы могут туннелировать, имея при этом полную (кинетическую плюс потенциальную) энергию, величина которой меньше потенциальной в области под барьером. Туннельный способ выхода электронов из металла носит название “автоэлектронная эмиссия”, т.е. эмиссия без затрат энергии, т.к. не надо совершать работу по преодолению барьера. Общая эмиссия при наличии электрического поля станет более интенсивной благодаря туннельному эффекту и увеличившемуся из-за понижения барьера надбарьерному выходу электронов. Такой совокупный вид эмиссии называется “термоавтоэлектронная эмиссия”. При относительно низких температурах (количественный критерий этому будет дан ниже) эмиссия электронов будет происходить с энергетических уровней, прилегающих к уровню Ферми.

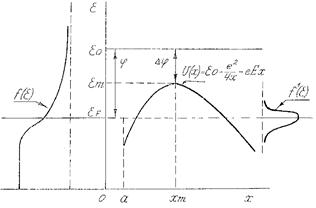
Рис. 2.5

На рис. 2.5 справа схематически изображена функция распределения f' (e) эмиттированных электронов. На уровнях вблизи энергии Ферми достаточно много электронов f (e _F)= ¹/₂ , а интенсивность туннельного эффекта больше, чем уже барьер. На энергетических уровнях, лежащих ниже уровня Ферми, много электронов, но барьер широк, а на уровнях выше вершины барьера очень мало электронов, хотя барьер не препятствует их выходу из металла. Таким образом, термоавтоэмиссия электронов из металла происходит в довольно узком диапазоне энергий. В силу этого в эмиссионной электронике вводят величину, называемую эмиссионной работой выхода или просто работой выхода

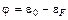. (2.8)

Ниже мы увидим, что эта величина играет определяющую роль при количественном описании явления эмиссии. Найдем положение вершины барьера. Из (2.6) и (2.7) следует

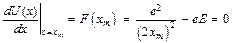, (2.9)

откуда

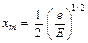(2.10)

и

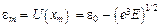(2.11)

Величина

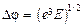(2.12)

носит название “поправка Шоттки” к работе выхода, а само понижение барьера на величину j при наличии электрического поля  “эффект Шоттки”.

В заключении данного параграфа отметим, что в приведенных выше рассуждениях молчаливо предполагалось, что эмиттирующая поверхность металла чистая и граничит с хорошим вакуумом. В реальных условиях так называемого технического вакуума имеются атомы и молекулы остаточного газа, которые осаждаются, или, другими словами, адсорбируются на поверхности металла, изменяя его свойства, в частности, работу выхода.

Дата добавления: 2014-01-06