Цилиндрическая электродная система

Перейдем к рассмотрению в приближении нулевых начальных скоростей случая, когда электроды системы представляют собой два бесконечно длинных коаксиальных цилиндра. Радиусы внутреннего и наружного цилиндров равны r ₁ и r ₂ соответственно. Пусть внутренний цилиндр является катодом. Из соображений симметрии следует, что в этом случае все величины зависят только от r. Поэтому будем решать задачу в цилиндрических координатах, в которых уравнение Пуассона принимает вид

(11.32)

или, используя формулу (11.16),

. (11.33)

Условие стационарности протекания тока в цилиндрическом диоде

, (11.34)

где 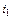 ток, проходящий через единицу длины диода. Тогда из (1.33) получим

. (11.35)

Будем искать решение этого уравнения в виде

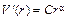, (11.36)

где С и a  постоянные величины. Подстановка (11.36) в (11.35) дает

. (11.37)

Так как правая часть уравнения (11.37) не зависит от r, то не должна от него зависеть и левая часть, т. е. a = ²/₃; но тогда

,

а следовательно, из (11.36) найдем

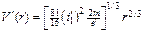. (11.38)

Подставляя сюда r = r ₂ и соответственно V' (r ₂) = V' _в, получим

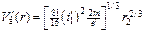, (11.39)

откуда

. (11.39а)

Полученная формула (11.39а) дает зависимость 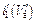такого же вида, как и формула (11.29) для плоского диода, только с другим численным коэффициентом. Однако между формулами (11.39а) и (11.29) есть и одно существенное различие. Оно состоит в том, что хотя функция (11.39) и является частным решением уравнения (11.32), она не удовлетворяет условию , а дает . Поэтому выражение (11.39) определяет не наименьшее значение 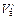, при котором возможен ток 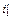, т. е. не значение , а значение 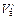, большее 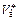. Вследствие этого полученная зависимость 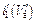не является вольт-амперной характеристикой цилиндрического диода. Однако найденное выражение (11.38) может быть использовано для получения искомого решения. Последнее было найдено С. А. Богуславским, а также Ленгмюром и Адамсом в 1923 г.

Обозначим через В коэффициент, стоящий в формуле (11.38) перед членом . Было показано, что решение, удовлетворяющее уравнению Пуассона и условию , можно представить в виде

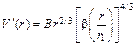. (11.40)

Функция была найдена в виде ряда

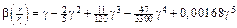
где . График функции приведен на рис. 11.6.

Из (11.40) находим

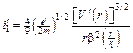. (11.41)

Тогда, подставляя в (11.41) r = r ₂, и функцию b при , получим вольт-амперную характеристику для этого случая:

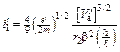. (11.42)

Из (11.42) прежде всего следует, что зависимость 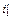от 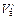та же, что и в предыдущем рассмотрении (при ) а именно, . Далее из графика , изображенного на рис. 11.6., следует, что значения 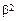заметно отличны от единицы только при небольших значениях r / r ₁ (меньших 10). При r / r ₁ ³ 10 значения 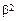отличаются от единицы не более, чем на несколько процентов. Поэтому ход потенциала в цилиндрическом диоде существенно отличается от хода, даваемого формулой (11.38), только вблизи катода при r, близких к r ₁. Что касается вольт-амперной характеристики, то поправочная функция 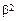пренебрежимо мало отличается от единицы, если r ₂/ r ₁ > 10. Различия между значениями 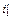, найденными из (11.39а) и (11.42), в этом случае меньше, чем отступления реального тока от вычисленного, из (11.42), вызываемые наличием распределения эмитированных электронов по скоростям, которое выше не учитывалось при выводе этих формул. Отметим, что из (11.42) вытекает сильная зависимость тока 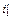от r ₂ и слабая зависимость от r ₁ (так как r ₁ находится под знаком логарифма).

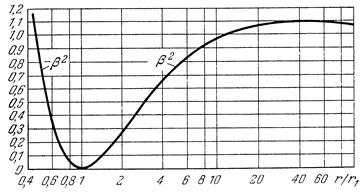
Рис. 11.6

Было показано, что решение (11.42) справедливо также и тогда, когда катодом является внешний цилиндр, а анодом  внутренний, т. е. когда r / r ₁ < 1. В этом случае для нахождения надо пользоваться левой частью графика , соответствующей этим значениям r / r ₁ (рис. 11.6).

Дата добавления: 2014-01-06