Влияние пространственного заряда на автоэлектронную эмиссию

Впервые вопрос о возможном влиянии пространственного заряда на автоэлектронную эмиссию был поднят вскоре после установления основного уравнения автоэлектронной эмиссии в работе Штерна, Госслинга и Фаулера.

Из уравнения Пуассона для распределения потенциала между бесконечными плоскими электродами следует

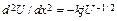, (11.45)

где U  потенциал; х  координата; k = 2p(2 m_e / e)^1/2; j  плотность тока. Решение этого уравнения с граничными условиями

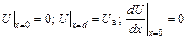, (11.46)

характерными для термоэлектронной эмиссии, приводит к известной формуле БогуславскогоЛенгмюра (11.29)

Для автоэлектронной эмиссии напряженность поля Е у поверхности эмиттера отлична от нуля и граничные условия (11.46) переходят в

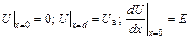(11.47)

Интегрируя (11.45) с учетом граничных условий (11.47), можно получить соотношение между напряженностью электрического поля, плотностью тока и потенциалом:

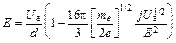. (E = (U _a/ d) [1  16/3p(2 m_e / e)^1/2 jU _a^1/2/ E ²]) (11.48)

Так как без учета пространственного заряда E = U _a/ d то критерий малости влияния этого заряда согласно (11.48) может быть записан в виде

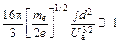. (16/3p(m_e /2 e)^1/2 jd / U _a^3/2<< 1) (11.49)

Правомерность выбранного одномерного приближения для реальной конфигурации диода с острийным катодом обосновывается тем, что пространственный заряд, оказывающий влияние на поле вблизи эмиттирующей поверхности, можно считать сосредоточенным на очень малом расстоянии от катода. Решая (11.48) совместно с уравнением ФаулераНордгейма

j = АE ²ехр ( В / E), (11.50)

где А = 1,54 × 10^6/j; В = 6,83 × 10⁷× j^3/2J(у), и исключая из (11.48) и (11.50) плотность тока j, можно получить выражение, связывающее напряженность поля Е с потенциалом U:

4 kAU _а^3/2ехр ( B / E)  3 U _а = 9 k ² A ² E ² d ²exp (2 B / E)  3 Ed. (11.51)

Совместно с (11.50) оно позволяет для ряда фиксированных значений Е рассчитать плотность тока в зависимости от приложенного напряжения. При малых Е из (11.51) следует обычная связь поля и потенциала при нулевом токе (E = U _a/ d). При очень больших Е преобладающими становятся экспоненциальные члены и, как нетрудно видеть, (11.51) сводится к уравнению (11.29).

Параметр d выбирается равным 1/b, где b  геометрический фактор, связывающий напряженность поля с потенциалом для плотностей тока, при которых влиянием пространственного заряда можно пренебречь.

На рис 11.7 приведен график зависимости плотности эмиссионного тока от напряжения. Кривая АСЕ рассчитана согласно (11.50) в отсутствие пространственного заряда; кривая ACD построена на основании уравнений (11.50) и (11.51) с учетом пространственного заряда, кривая BD представляет закон БогуславскогоЛенгмюра (11.29). Как можно видеть, при малых U начальный участок кривой совпадает с прямой ФаулераНордгейма. При увеличении U кривая начинает отклоняться вниз и, наконец, асимптотически приближается к кривой БогуславскогоЛенгмюра.

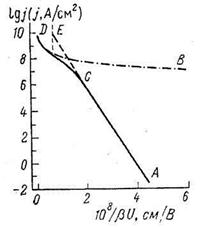
Рис 11.7. Теоретическая зависимость плотности тока автоэмиссии от приложенного напряжения.

Дата добавления: 2014-01-06