Ієрархічні алгоритми

Методи кластерного аналізу

Методи кластерного аналізу можна розділити на дві групи:

· Ієрархічні;

· Неієрархічні.

Кожна з груп включає безліч підходів і алгоритмів. Використовуючи різні методи кластерного аналізу, аналітик може отримати різні рішення для одних і тих же даних. Це вважається нормальним явищем.

Суть ієрархічної кластеризації полягає в послідовному об'єднанні менших кластерів в більші або поділі великих кластерів на менші.

Ієрархічні агломеративні методи (Agglomerative Nesting, AGNES). Ця група методів характеризується послідовним об'єднанням вихідних елементів і відповідним зменшенням числа кластерів.

На початку роботи алгоритму всі об'єкти є окремими кластерами. На першому кроці найбільш схожі об'єкти об'єднуються в кластер. На наступних кроках об'єднання продовжується до тих пір, поки всі об'єкти не будуть складати один кластер.

Ієрархічні дівізімні (подільні) методи (DIvisive ANAlysis, DIANA). Ці методи є логічною протилежністю агломеративним методам. В початку роботи алгоритму всі об'єкти належать одному кластеру, який на наступних кроках ділиться на менші кластери, в результаті утворюється послідовність розщеплюють груп.

Принцип роботи описаних вище груп методів у вигляді дендрограмми показаний на рис. 1.2.

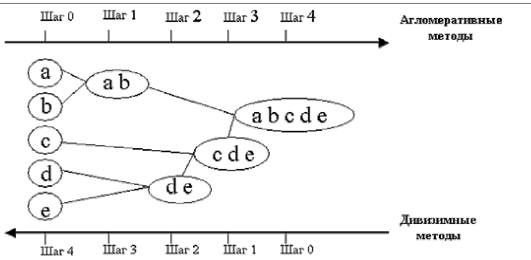
Рис. 1.2. Дендрограмма агломератівних і дівізімних методів

Ієрархічні методи кластеризації розрізняються правилами побудови кластерів. В якості правил виступають критерії, які використовуються при вирішенні питання про "Схожості" об'єктів при їх об'єднанні в групу (агломератівние методи) або поділу на групи (дівізімние методи).

Ієрархічні методи кластерного аналізу використовуються при невеликих обсягах наборів даних. Перевагою ієрархічних методів кластеризації є їх наочність.

Ієрархічні алгоритми пов'язані з побудовою дендрограм (від грецького dendron - "Дерево"), які є результатом ієрархічного кластерного аналізу. Дендрограма описує близькість окремих точок і кластерів один до одного, представляє в графічному вигляді послідовність об'єднання (поділу) кластерів.

Дендрограма (dendrogram) - деревоподібна діаграма, що містить n рівнів, кожен з яких відповідає одному з кроків процесу послідовного укрупнення кластерів. Дендрограма також називають деревоподібної схемою, деревом об'єднання кластерів, деревом ієрархічної структури. Дендрограма являє собою вкладену угруповання об'єктів, яка змінюється на різних рівнях ієрархії. Існує багато способів побудови дендограм. У дендограмі об'єкти можуть розташовуватися вертикально або горизонтально. Приклад вертикальної дендрограми наведено на рис. 1.3.

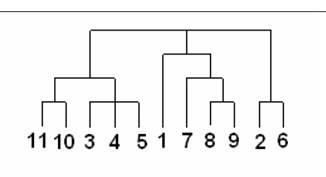
Рис. 1.3. Приклад дендрограмми

Числа 11, 10, 3 і т.д. відповідають номерам об'єктів або спостережень вихідної вибірки. Ми бачимо, що на першому кроці кожне спостереження являє один кластер (вертикальна лінія), на другому кроці спостерігаємо об'єднання таких спостережень: 11 і 10; 3, 4 і 5; 8 і 9; 2 і 6. На другому кроці продовжується об'єднання в кластери:

спостереження 11, 10, 3, 4, 5 і 7, 8, 9. Даний процес продовжується до тих пір, поки всі спостереження не об'єднаються в один кластер.

нехай

K_i - i-я група (клас, кластер), що складається з n об'єктів;

x_i - середнє арифметичне векторних спостережень Ki групи, тобто «центр тяжкості» i - ої групи;

r (K_i, K _j) = r_ij - відстань між групами K_i і K _j.

Узагальнена алгомератівная процедура. На першому кроці кожен об'єкт вважається окремим кластером. На наступному кроці поєднуються два найближчих об'єкта, які утворюють новий клас, визначаються відстані від цього класу до всіх інших об'єктів, і розмірність матриці відстаней D скорочується на одиницю. На p -му кроці повторюється та ж процедура на матриці D _{(n-p) (n-p)}, поки всі об'єкти не об'єднаються в один клас.

Якщо відразу кілька об'єктів (класів) мають мінімальну відстань, то можливі дві стратегії: вибрати одну випадкову пару або об'єднати відразу всі пари. Перший спосіб є класичним і реалізований у всіх процедурах (іноді його називають висхідній ієрархічної класифікації). Другий спосіб називають методом найближчих сусідів (не плутати з алгоритмом "Найближчого сусіда") і використовують рідше.

У даній статті буде використовуватися метод нечіткої кластеризації c-means. Відмінною особливістю нечіткої кластеризації є той факт, що кожен об'єкт може відноситися до кожного кластеру з певним ступенем належності.

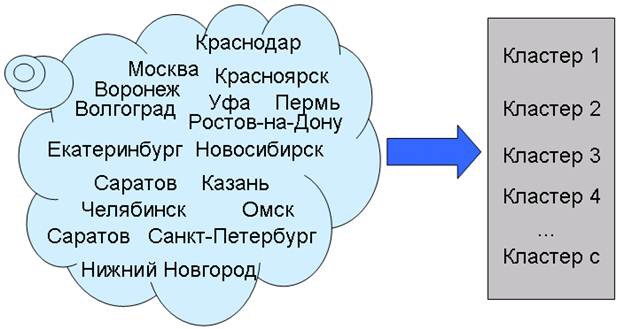
Для аналізу будуть обрані 17 найбільших міст Росії по населенню, в якості характеристик виступають соціально-економічні показники (демографія, зайнятість населення, зарплата, злочинність і т.д.). Результатом будуть отримані кластери міст.

Дата добавления: 2014-01-06