
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 5. Тема 6. Информационные и инфокоммуникационные процессы и средства (продукты, системы, сети и технологии) сравнение информапционных и материальных средств и
|
|
|
|
Тема 6. Информационные и инфокоммуникационные процессы и
средства (продукты, системы, сети и технологии)
СРАВНЕНИЕ ИНФОРМАПЦИОННЫХ И МАТЕРИАЛЬНЫХ СРЕДСТВ И ПРОЦЕССОВ (ПРОДУКТОВ, СИСТЕМ, СЕТЕЙ, ТЕХНОЛОГИЙ)
| СХОДСТВО | ОТЛИЧИЕ |
| 1. Продукт не есть товар | 1. Один материальный продукт существует в единственном экземпляре. Один информационный продукт допускает множественное существование |
| 2. Каждая операция материального и информационного технологических процессов содержит как рабочие, так и контрольные функции | 2. На выходе материального технологического процесса из объема исходного сырья (заготовки), необходимого для изготовления одного продукта, может быть получен только один такой же продукт, а на выходе информационного – много, причем одинакового или разного назначения, функций, качества и т.п. |
| 3. Оба технологических процесса допускают распараллеливание и совмещение во времени и пространстве выполнения отдельных операций | 3. Возможности одновременно совмещаемых операций в информационных технологических процессах шире и глубже, операции допускают как горизонтальное, так и вертикальное распараллеливание |
| 4. Обращение с продуктами и способами допускает правовую охрану | 4. Имеются принципиальные отличия в правовой охране объектов материальной и интеллектуальной (как продукта информационных техпроцессов) собственности, имущественных и неимущественных прав на них |

| Вид носителей информации | Аналоговые | Цифровые | Когнитивные (интеллектуальные 1-го типа) | Нейронные (интеллектуальные 2-го типа) |
| Гибридные, комбинированные | ||||
| Тип носителя (форма представления информации) | Физические сигналы | Данные, анзния, математические модели, контент | Явные знания, протознания | Неявные, неформализованные «знания», приобретенные в процессе самообучения, опыт |
| Принцип действия | Структурный (аппаратный, аналитический, аналоговый) | Алгоритмический | Логический, исчислительно-селективный по правилам | Структурно-логический по алгоритму (правилам) «учителя» |
| Вид преобразований | Непрерывные во времени, непрерывнозначные | Дискретные во времени, цифровые | Квантовые | Дискретные, операторные |
| Вид структуры | Жесткая | Программно-перестраиваемая | Перестраиваемая | Жесткая, перестраиваемая при обучении |
| Элементарные операции с операндами | Количественные | Качественные | Качественные | Количественные |
| Базовые информационные операции | Измерительные | Вычислительные, логические | Исчислительные выводы | Измерительно-вычислительные |
| Показатели качества результатов | Точность | Адекватность | Достоверность, уверенность, истинность |
Разновидности технических средств информатики

|
Морфологическая таблица информационных систем и сетей
| Главные факторы, определяющие структуру | Отличительный признак | Возможные реализации признака | |||||
| i | y i | k | p i k | 1 P i k | 2 P i k | 3 P i k | 4 P i k |
| Выполняемые функции | Класс решаемых задач | Управленческие | Вычислительные | Измерительные | Прочие | ||
| Количество решаемых разнотипных задач (достигаемых целей) | Специализиро-ванные (одноце-левые) | Многоцелевые | — | ||||
| проблемно (пред-метно) ориентированные | универсальные | ||||||
| Количество функций, выполняемых в рамках одного направления (цели) | Однофункцио-нальные (узко-специализиро-ванные) | Многофункцио-нальные | — | — | |||
| Организация выработки информации, представляемой пользователю | Способ выработки информации | Интровертные | Экстравертные | ||||
| Добывающие | Получающие (передающие) | Хранящие (вос-производящие) | «Генерирующие» (преобразующие) | ||||
| Организация ввода и накопления исходных данных | Наличие предварительной регистрации | Без предварительной регистрации | С предварительной регистрацией | — | |||
| всех данных | части данных | ||||||
| Наличие накопления данных перед обработкой | Без накопления | С накоплением | — | — | |||
| Размерность исходных данных, операндов, результатов | Количество одновременно вводимых массивов данных (сигналов) | Одновходовые | Многовходовые (n-входовые), n >1 | — | — | ||
| Размерность обрабатываемых массивов и получаемых результатов | Одномерные | Многомерные, векторные (k -мерные), k >1 | — | — |
Продолжение таблицы
| Главные факторы, определяющие структуру | Отличительный признак | Возможные реализации признака | |||||
| i | y i | k | p i k | 1 P i k | 2 P i k | 3 P i k | 4 P i k |
| Архитектурно-структурное решение всей системы | Иерархичность | Одноуровневые | Многоуровневые | — | — | ||
| Расстояние между элементами ИС | Сосредоточенные (локальные) | Распределенные | — | — | |||
| Сходство элементов аналогичного назначения | Однородные | Неоднородные | — | — | |||
| Архитектурно-структурное решение вычислительных преобразований | Организация потоков команд и данных | Однокомандные | Многокомандные | ||||
| ОКОД (SISD) (последовательные) | ОКМД (SIMD) (матричные, ассоциативные) | МКОД (MISD) (конвейерные, магистральные) | МКМД (MIMD) (многопроцессорные) | ||||
| Принцип распараллеливания вычислений и выполняемых функций | Без распараллеливания | С распараллеливанием | — | ||||
| Аппаратное | Программное | ||||||
| Организация управления и перестройки | Способ управления | Аппаратный | Программный | — | — | ||
| Автоматизация перестройки | Ручная | Автоматизированная | Автоматическая | — | |||
| Централизация управления | Централизован-ные: глобальная и локальная централизация (оди-ночные простые системы) | Децентрализо-ванные: глобальная и локальная автономия (множество, набор систем) | Смешанные | ||||
| Глобальная централизация, локальная автономия (сети) | Глобальная автономия, локальная централизация (ИС в виде коллектива подсистем) | ||||||
| Учет вариаций, внешних воздействий и окружающей среды. Уровень самоперестройки | Неадаптивные (неперестраивающиеся) | Адаптивные (самоприспосабливающиеся) | |||||
| Самоперестраивающиеся | Самообучающиеся | Самоорганизующиеся |
Окончание таблицы
| Главные факторы, определяющие структуру | Отличительный признак | Возможные реализации признака | |||||
| i | y i | k | p i k | 1 P i k | 2 P i k | 3 P i k | 4 P i k |
| Элементная база | Физический принцип действия | Электронные | Оптические | Механические | Прочие | ||
| Форма представления информации | Аналоговые | Цифровые | Гибридные | — | |||
| Принцип выполнения вычислительных преобразований | Детерминирован-ные | Стохастические | — | — | |||
| Исполнение | Возможность агрегатирования | Неагрегатируемые | Агрегатируемые | ||||
| Стандартизация, унификация, совместимость со смежными средствами | Несовместимые | Совместимые по функциональным параметрам | |||||
| информационно | метрологически | ||||||
| Совместимые по элементной базе | |||||||
| аппаратно | программно | ||||||
| Совместимые по внешним параметрам | |||||||
| конструктивно | энергетически | эксплуатационно |
Примечание.
ОКОД – один поток команд, один поток данных (одни команды, одни данные) /SISD – single instruction single data/ – архитектура фон Неймана;
ОКМД – один поток команд, много потоков данных /SIMD – single instruction multiple data/;
МКОД – много (потоков) команд, один поток данных /MISD – multiple instruction single data/;
МКМД – много потоков команд, много потоков данных /MIMD – multiple instruction multiple data/.
См. также Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002. – 608 с.
Губарев В.В. Информатика: прошлое, настоящее, будущее. – М.: Техносфера, 2011. – 432 с.

Топологические структуры информационных сетей:
а – радиальная; б – кольцевая (петлевая); в – полносвязная; г – радиально-кольцевая; д – древовидная; е – звездообразная;
ж – последовательная; з – магистральная; и – кустовая с тремя деревьями; к-м – сетевая; – узел возможного переключения
направления информационного потока; – узел без переключения направления информационного потока
ПОЯСНЕНИЕ ПРИНЦИПОВ РАБОТЫ ИНФОРМАЦИОННЫХ СРЕДСТВ [1]
(на примере вычислительных средств)
Пример первый
Необходимо найти значение определенного интеграла  . (1)
. (1)
Рассмотрим, как найти его значение на ВМ различных типов.
Аналоговый принцип операционного типа. Для этого необходимо  заменить на
заменить на  , т.е. выбрать масштабные коэффициенты преобразования х в t и f в
, т.е. выбрать масштабные коэффициенты преобразования х в t и f в 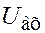 , установить RC пропорциональным b-a и определить
, установить RC пропорциональным b-a и определить 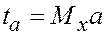 и
и 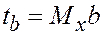 , учитывая масштабы
, учитывая масштабы  и
и 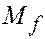 . Затем собрать и запустить схему, подав на ее вход
. Затем собрать и запустить схему, подав на ее вход  , начиная с
, начиная с  , и измерить значение
, и измерить значение 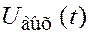 в момент
в момент 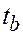 (см. слайд 4).
(см. слайд 4).
Цифровой принцип. При цифровом принципе вычислений значения интеграла I находятся путем численного интегрирования. Диапазон  аргумента х разбивается на п состыкованных участков шириной D х так, чтобы заштрихованные площадки участков могли быть легко вычислены с требуемой точностью как площади, заменяющие эти участки прямоугольниками, трапециями или другими приемами численного интегрирования.
аргумента х разбивается на п состыкованных участков шириной D х так, чтобы заштрихованные площадки участков могли быть легко вычислены с требуемой точностью как площади, заменяющие эти участки прямоугольниками, трапециями или другими приемами численного интегрирования.
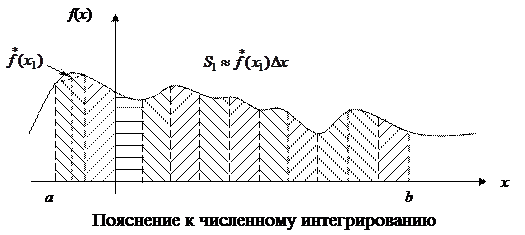 Когнитивные принципы. Идея работы ВМ, основанных на когнитивных принципах: использование явных знаний, хранимых в памяти или выдаваемых экспертами. В данном случае в качестве явных знаний выступают таблицы определенных или неопределенных интегралов, хранимых в памяти. Интеграл сводится к табличному, из которого находится первообразная
Когнитивные принципы. Идея работы ВМ, основанных на когнитивных принципах: использование явных знаний, хранимых в памяти или выдаваемых экспертами. В данном случае в качестве явных знаний выступают таблицы определенных или неопределенных интегралов, хранимых в памяти. Интеграл сводится к табличному, из которого находится первообразная 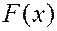 . Далее, подставляя в
. Далее, подставляя в 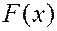 конкретные числа а и b, определяем искомое значение интеграла I методами цифровых вычислений.
конкретные числа а и b, определяем искомое значение интеграла I методами цифровых вычислений.
Нейросетевой (нейрокомпьютерный) принцип. Нейросетевые принципы базируются на двух идеях: 1) построение сети из k слоев, в каждом из которых по 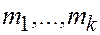 нейронных элементов, образующих сеть типа одной из изображенных на слайде, использование неявных, приобретенных в ходе самообучения сети, знаний в виде коэффициентов
нейронных элементов, образующих сеть типа одной из изображенных на слайде, использование неявных, приобретенных в ходе самообучения сети, знаний в виде коэффициентов  каждого из элементов. В рассматриваемом примере обучение сводится к установлению значений
каждого из элементов. В рассматриваемом примере обучение сводится к установлению значений  по большому числу разнообразных функций
по большому числу разнообразных функций  , т.е. по значениям
, т.е. по значениям 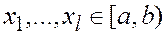 и
и  , для которых значение интеграла I (площади кривых на
, для которых значение интеграла I (площади кривых на  ) заранее известны. Тогда, подавая на входы сети значения х и
) заранее известны. Тогда, подавая на входы сети значения х и  для интеграла, получаем искомый результат, как следствие приобретенного ранее опыта, неявных знаний.
для интеграла, получаем искомый результат, как следствие приобретенного ранее опыта, неявных знаний.
Стохастический принцип. Все предыдущие принципы относятся к детерминированным. Идея стохастического принципа – использование метода статистических испытаний Монте-Карло или оценивание математического ожидания через среднее арифметическое большого числа выборочных значений (реализаций) 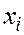 случайных величин, векторов или функций. В рассматриваемом примере I есть математическое ожидание М {Х} абсолютно непрерывной случайной величины Х с равномерным на
случайных величин, векторов или функций. В рассматриваемом примере I есть математическое ожидание М {Х} абсолютно непрерывной случайной величины Х с равномерным на 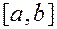 законом распределения, т.е.
законом распределения, т.е.
 . (2)
. (2)
Правая часть есть оценка I, которая тем точнее, чем больше N – объем выборки. Это означает, что с помощью датчика равномерно распределенных на 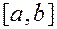 случайных величин, имеющихся в современных ПЭВМ, или из таблицы случайных (псевдослучайных) равномерно распределенных и приведенных к
случайных величин, имеющихся в современных ПЭВМ, или из таблицы случайных (псевдослучайных) равномерно распределенных и приведенных к  чисел выбираются
чисел выбираются 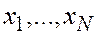 и по формуле
и по формуле  находится приближенное значение интеграла I. Метод особенно хорош, если, во-первых, функция
находится приближенное значение интеграла I. Метод особенно хорош, если, во-первых, функция 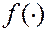 имеет сложный вид, трудно аналитически или численно интегрируемая, и, во-вторых, интеграл I многомерный. В этом случае приближение зависит прежде всего не от кратности интеграла (в отличие от численного интегрирования), а от объема выборки N, т.е. от временных затрат.
имеет сложный вид, трудно аналитически или численно интегрируемая, и, во-вторых, интеграл I многомерный. В этом случае приближение зависит прежде всего не от кратности интеграла (в отличие от численного интегрирования), а от объема выборки N, т.е. от временных затрат.
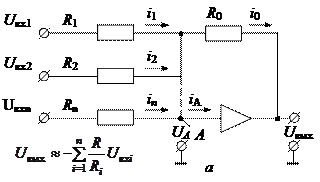 | ||||||||
 | ||||||||
 | ||||||||
 | ||||||||
 |
Рис. П4.1. Схемы различных вариантов решающих усилителей и математические модели, описывающие переходные процессы в них:
а – суммирующий; б – интегрирующий; в – интегрирующий сумму входных напряжений; г – интегрирующий с заданием
начальных условий; д – дифференцирующий; R – резисторы (сопротивлением R), С – конденсаторы (емкостью С)
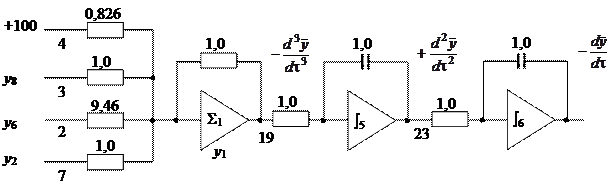 | |||||
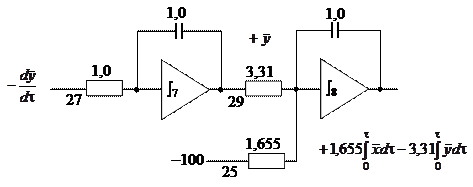 | |||||
 |
Рис. П4.2. Наборная схема для решения дифференциального уравнения
(нумерацию входов и выходов резисторов и усилителей для коммутации см. на рис. П4.1)

Рис. П4.3. Общий вид наборного поля аналоговой вычислительной машины МН-7; при сопротивлении резистора обратной связи R 0 = 1 Мом переменные резисторы (их сопротивления) № 4,8,12,16,20,24,28,32,36,40,44 и 48 служат
для плавной установки передаточных коэффициентов (они указываются на наборной схеме как отношение R 0/ Ri)
в пределах от 0 до 1, резисторы № 2,6,10,14,18,22,26,30,34,38,42 и 46 – от 0 до 10
Пример второй
Необходимо найти значение  . (3)
. (3)
Аналоговый принцип. Значение y находим с помощью нелинейного электронного блока АВМ, преобразующего входное напряжение 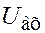 в выходное
в выходное 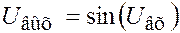 . Иными словами, как и в первом примере, устанавливаем
. Иными словами, как и в первом примере, устанавливаем 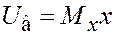 , измеряя, подаем его на вход нелинейного синусоидального блока и, спустя время переходных процессов, измеряем
, измеряя, подаем его на вход нелинейного синусоидального блока и, спустя время переходных процессов, измеряем 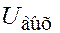 , которое с соответствующим масштабным коэффициентом дает нам y.
, которое с соответствующим масштабным коэффициентом дает нам y.
Понятно, что, как и в первом примере, точность нахождения y имеет принципиальные ограничения, поскольку определяется тем, что аналоговый принцип связан с выполнением количественных операций: измерением напряжений, точностью выполнения преобразований  и
и 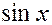 в блоках, колебаниями источников питания, шумами и помехами в блоках АВМ, «уходом» значений параметров схем от номинальных и т.д. Зато быстродействие определяется только переходными процессами в блоках АВМ и просто осуществляется визуализация результатов.
в блоках, колебаниями источников питания, шумами и помехами в блоках АВМ, «уходом» значений параметров схем от номинальных и т.д. Зато быстродействие определяется только переходными процессами в блоках АВМ и просто осуществляется визуализация результатов.
Цифровой принцип. Функция, описывающая зависимость  , разлагается в ряд простейших функций, например, Маклорена
, разлагается в ряд простейших функций, например, Маклорена
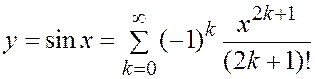 . (4)
. (4)
Затем для требуемого х по правой части находится значение y. Понятно, что точность нахождения y будет зависеть от разрядности представления х, а также количества используемых слагаемых в сумме (å) правой части. Иными словами, здесь, в силу качественного принципа выполнения операций, нет принципиальных ограничений по точности: надо только брать больше разрядов х и больше слагаемых, что, конечно, приводит к потере производительности, требует алгоритмизации и программирования, зато цифровые элементы существенно меньше подвержены колебаниям напряжений, шумам и помехам, допускают использование помехоустойчивых операций и т.д.
Когнитивный принцип. В этом случае для требуемого 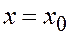 значение y находится по таблице синусов, выбираемой из памяти. Если же в таблице нет значений
значение y находится по таблице синусов, выбираемой из памяти. Если же в таблице нет значений  , а есть только значения
, а есть только значения 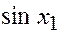 и
и 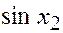 для
для  , то значение
, то значение 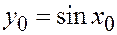 находится приближенно через
находится приближенно через  и
и  , считываемые из базы знаний, с помощью ЦВМ одним из численных методов, например, с применением интерполяции
, считываемые из базы знаний, с помощью ЦВМ одним из численных методов, например, с применением интерполяции
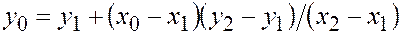 . (5)
. (5)
Привести пример аналоговых, цифровых и когнитивных систем связи, указать их достоинства и недостатки.
Нейросетевой принцип. Аналогично предыдущему примеру, вначале происходит обучение сети получению  для разных
для разных  , а затем определяется
, а затем определяется 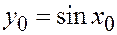 , подачей на вход сети
, подачей на вход сети  и вида функции –
и вида функции – 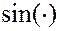 .
.
В заключение обратим внимание, что аналоговые принципы вычислений являются как бы обратными по отношению к гносеологическому (познавательному) моделированию. При познавательном моделировании первично модель подбирается под физический процесс, а при аналоговом моделировании – процесс (и обеспечивающие его протекание средства) подбираются под модель, под заданную вычислительную задачу. В аналоговых средствах осуществляется не вычисление, а его замена, эмуляция вычисления с использованием аналогии, подобия и измерения.
[1] См. Губарев В.В. Информатика: прошлое, настоящее, будушее. – М.: Техносфера, 2011. – 432 с.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 404; Нарушение авторских прав?; Мы поможем в написании вашей работы!