Вынужденные колебания в электрическом колебательном контуре. Резонанс. Резонансные кривые

Backward

Right

Left

Turtle.forward 100

Import turtle – подключает библиотеку с черепашкой.

Команды для черепахи

Интерплитация.

Метод пошаговой детализации.

Ремонт комнаты

Ремонт комнаты

Потолок
Стены
Пол

Ремонт кухни

Ремонт с/у

Ремонт кор.

Компиляция - процесс перевода текста программы в машинный код.

Turtle.reset()

Home()
dot(размер,цвет)
circle(r,угол,кол.шагов)
undo отмена последнего шага
penup не рисует но ползет
prndown опять рисует
pencolor веет ручки
fillcolor заливка
begin_fill
end_fill
clear очистка
bgcolor заливка фона

Чтобы в реальной электрическом колебательном контуре получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью вынуждающей силы - внешней эдс, изменяющейся по гармоническому закону:

U = U_m cos wt.

Согласно второму правилу Кирхгофа, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор R и в котором действует внешняя эдс можно записать

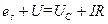или (1)

где U_c = = q/C — напряжение на конденсаторе, e_s - э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока, IR – падение напряжения на сопротивлении. Следовательно, уравнение (2) можно привести к виду

,

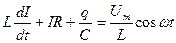или разделив на L при учете, что I=dq/dt, а dI/dt=d²q/dt² получим дифференциальное уравнение колебаний заряда q в контуре или дифференциальное уравнение свободных затухающих колебаний заряда q в контуре:

(2)

Такое уравнение известно из курса механики

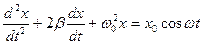(3)

Здесь b- коэффициент затухания, w₀ - циклическая частота собственных колебаний.

, .

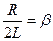В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими. Решение уравнения (3) для установившегося режима имеет вид

.

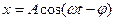Причем амплитуда A и фаза j зависят от w, w₀, b, x ₀

,

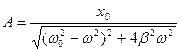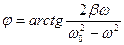
В соответствии с этими формулами для (2) запишем

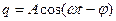
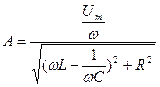(4)

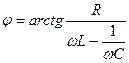(5)

Амплитудные резонансные кривые построенные на основе (4), приведены на рис.1.

Явление резкого возрастания амплитуды вынужденных колебаний на некоторой частоте, называемой резонансной (которая для малого затухания совпадает с частотой собственных колебаний w₀) называется резонансом.

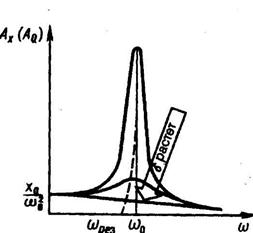
Рис.1.

Чем больше коэффициент затухания, тем ниже амплитуда при резонансе.

Статическое отклонение (при w стремящейся к нулю) равно 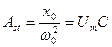, а амплитуда при резонансе, т.е. они связаны через добротность Q

A_res=QA_st,, где 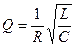. Чем выше добротность контура, тем выше амплитуда при резонансе.

Фазовая резонансные кривые построенные на основе (5), приведены на рис.2.

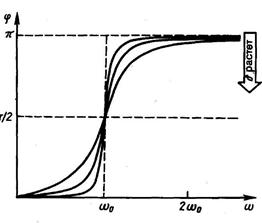
Рис.2.

Видно, что только в случае когда затухания нет (b=0), вынуждающая сила и колебания совпадают по фазе.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных, колебаний прибора. Так, радиотехника, прикладная акустика, оборудование, воспринимающее электрические колебания, основаны на явлении резонанс.

Дата добавления: 2014-01-06