
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямая и обратная задачи кинематики
|
|
|
|
Кинематическое уравнение движения
Как было указано выше в п. 1.3, характер движения точки и вид ее траектории описывают кинематическими уравнениями движения  , { x (t), y (t), z (t)}, которые однозначно определяют положение материальной точки в любой момент времени t относительно выбранной системы отсчета.
, { x (t), y (t), z (t)}, которые однозначно определяют положение материальной точки в любой момент времени t относительно выбранной системы отсчета.
При решении конкретных задач кинематики могут возникать две принципиально различные ситуации в зависимости от того, какая информация известна о движении точки.
1. Прямая задача кинематики. Известен математический вид кинематического уравнения движения. Необходимо найти кинематические характеристики 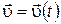 и
и 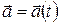 . В этом случае задача однозначно решается с помощью (1.5), (1.6), (1.14), (1.15).
. В этом случае задача однозначно решается с помощью (1.5), (1.6), (1.14), (1.15).
2. Обратная задача кинематики. Известна одна из кинематических характеристик движения как функция времени (например, 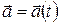 ). Необходимо определить остальные кинематические величины:
). Необходимо определить остальные кинематические величины: 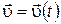 и кинематическое уравнение движения
и кинематическое уравнение движения 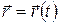 . В этом случае однозначное решение задачи может быть найдено только при наличии дополнительной информации. Должны быть известны кинематические величины
. В этом случае однозначное решение задачи может быть найдено только при наличии дополнительной информации. Должны быть известны кинематические величины  и
и  в некоторый момент времени t 0, условно принятый за начальный. Величины
в некоторый момент времени t 0, условно принятый за начальный. Величины  и
и  называются начальными условиями задачи. Тогда с помощью (1.14) будем иметь
называются начальными условиями задачи. Тогда с помощью (1.14) будем иметь
 .
.
Интегрируя в пределах от t 0 до t, получим
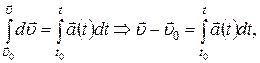
то есть
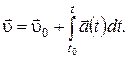 (1.35)
(1.35)
Кинематическое уравнение движения найдем на основании (1.5) с учетом (1.35)
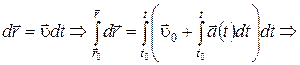
 (1.36)
(1.36)
В качестве примера рассмотрим решение обратной задачи о движении точки с постоянным ускорением  . В этом случае из (1.32) име-
. В этом случае из (1.32) име-
ем
 , (1.37)
, (1.37)
а из (1.36)
 . (1.38)
. (1.38)
Выводы: В кинематике встречаются два типа задач: прямая и обратная. Прямая задача имеет однозначное решение. Обратная задача для однозначности решения требует знания начальных условий.
Контрольные вопросы
1.11. Покажите, что движение с  происходит в одной плоскости, а траектория точки в этой плоскости представляет ветвь параболы.
происходит в одной плоскости, а траектория точки в этой плоскости представляет ветвь параболы.
1.12. Покажите, что вращательное движение материальной точки вокруг неподвижной оси с постоянным угловым ускорением  описывается кинематическими уравнениями
описывается кинематическими уравнениями
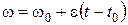 , (1.39)
, (1.39)
 , (1.40)
, (1.40)
где 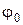 и
и  значения
значения  и
и 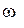 при
при  .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 14054; Нарушение авторских прав?; Мы поможем в написании вашей работы!