Ориентирование по географическому меридиану точки

Ориентирование линий

Ориентировать линию - значит определить ее направление относительно другого направления, принятого за начальное. Направление определяется величиной ориентирного угла, то есть, угла между начальным направлением и направлением линии.

В геодезии за начальное направление принимают:

• географический меридиан точки,
• осевой меридиан зоны,
• магнитный меридиан точки.

Географическим азимутом называется угол, отсчитанный по ходу часовой стрелки от северного направления географического меридиана точки до направления линии; он обозначается буквой A (рис.1.11). Пределы изменения географического азимута от 0^o до 360^o.

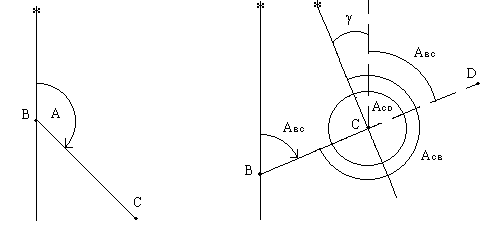
Рис.1.11 Рис.1.12

Азимут прямой линии в разных ее точках имеет разные значения, так как меридианы на поверхности сферы непараллельны между собой. Проведем линию BC и меридианы в точках B и C (рис.1.12). Азимут этой линии в точке C отличается от азимута линии в точке B на величину сближения меридианов точек B и C:

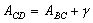(1.9)

В геодезии различают прямое и обратное направление линии. Например, в точке C линии BD прямое направление - направление CD, обратное направление - направление CB. Прямой и обратный азимут линии в одной точке различаются ровно на 180^o, однако, для разных точек линии это равенство не выполняется. Пусть BC - прямое направление линии в ее начале (в точке B), A_BC - азимут прямого направления; CB - обратное направление линии в ее конце (в точке C), A_CB - азимут обратного направления, тогда

(1.10)

то есть, обратный азимут линии равен прямому азимуту плюс-минус 180^o, плюс сближение меридианов точек начала и конца линии.

Различают восточное (положительное) и западное (отрицательное) сближение меридианов. Если конечная точка линии находится к востоку от начальной, то сближение меридианов будет восточным и положительным; если конечная точка линии лежит к западу от начальной, то сближение меридианов будет западным и отрицательным.

Формула сближения меридиана. На сфере наметим две точки A и B, лежащие на одной параллели, то есть, имеющие одинаковую широту (рис.1.13).

Рис.1.13

Проведем на поверхности сферы экватор и параллель точек A и B; в плоскости параллели проведем радиусы параллели FA = r и FB = r; угол между ними равен разности долгот точек.

Через точки A и B проведем полуденные линии AN и BN, которые, пересекаясь на продолжении оси вращения Земли, образуют угол γ, являющийся сближением меридианов точек A и B. Требуется выразить Рис.1.13 угол γ через координаты точек A и B, то есть, через широту φ и долготы λ_A и λ_B, причем Δλ = λ_B - λ_A.

Выразим длину дуги AB двумя способами: из ΔABN AB = BN * γ и из ΔABF AB = r * Δλ (углы γ и Δ λ выражены в радианах). Далее пишем:

BN*γ=r* Δλ, (1.11)
откуда
. (1.12)

Радиус параллели выразим из Δ OFB r = R*Cos(φ), а отрезок BN - из ΔONB BN = R * Ctg(φ), где R - радиус сферы; тогда

γ = Δ λ * Sin(φ)
или

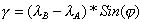(1.13)

В этой формуле размерность γ соответствует размерности λ.

Гауссово сближение меридианов. Частным случаем сближения меридианов является гауссово сближение меридианов, когда начальная точка A лежит на осевом меридиане зоны. Величина гауссова сближения меридианов, равного сближению меридиана точки и осевого меридиана зоны, является одной из характеристик положения точки внутри зоны. Формула гауссова сближения меридианов имеет вид

(1.14)

Буквами L и B здесь обозначены геодезические долгота и широта точки, буквой L₀ - долгота осевого меридиана зоны. В пределах зоны гауссово сближение меридианов не может превышать величины 3^o*Sin(B).

Дата добавления: 2014-01-06