Вычисление координат пунктов разомкнутого линейно-углового хода

Классификация линейно-угловых ходов

Для определения координат нескольких точек можно применить различные способы; наиболее распространенными из них являются линейно-угловой ход, система линейно-угловых ходов, триангуляция, трилатерация и некоторые другие.

Линейно-угловой ход представляет собой последовательность полярных засечек, в которой измеряются горизонтальные углы и расстояния между соседними точками (рис.2.17).

Рис.2.17. Схема линейно-углового хода

Исходными данными в линейно-угловом ходе являются координаты X_A, Y_A пункта A и дирекционный угол α_BA линии BA, который называется начальным исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B.

Измеряемые величины - это горизонтальные углы β₁, β₂,..., β_k-1, β_k и расстояния S₁, S₂, S_k-1, S_k. Известны также ошибка измерения углов m_β и относительная ошибка измерения расстояний m_S / S = 1 / T.

Дирекционные углы сторон хода вычисляют последовательно по известным формулам передачи дирекционного угла через угол поворота

для левых углов: (2.64)

для правых углов: 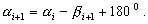(2.65)

Для хода на рис.2.17 имеем:

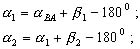
и т.д.

Координаты пунктов хода получают из решения прямой геодезичекой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.

Линейно-угловой ход, изображенный на рис.2.17, применяется очень редко, так как в нем отсутствует контроль измерений; на практике, как правило, применяются ходы, в которых предусмотрен такой контроль.

По форме и полноте исходных данных линейно-угловые ходы подразделяются на следующие виды:

1. разомкнутый ход (рис.2.18): исходные пункты с известными координатами и исходные дирекционные углы есть в начале и в конце хода;

Рис.2.18. Схема разомкнутого линейно-углового хода

Если в начале или в конце хода нет исходного дирекционного угла, то это будет ход с частичной координатной привязкой; если исходных дирекционных углов в ходе совсем нет, то это будет ход с полной координатной привязкой.

1. замкнутый линейно-угловой ход (рис.2.19) - начальный и конечный пункты хода совмещены; один пункт хода имеет известные координаты и называется исходным пунктом; на этом пункте должно быть исходное направление с известным дирекционным углом, и измеряется примычный угол между этим направлением и направлением на второй пункт хода.

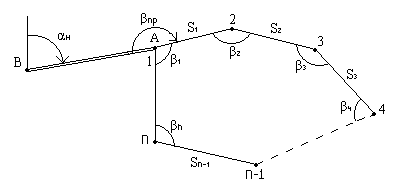
Рис.2.19. Схема замкнутого линейно-углового хода

1. висячий линейно-угловой ход (рис.2.17) имеет исходный пункт с известными координатами и исходный дирекционный угол только в начале хода.
2. свободный линейно-угловой ход не имеет исходных пунктов и исходных дирекционных углов ни в начале, ни в конце хода.

По точности измерения горизонтальных углов и расстояний линейно-угловые ходы делятся на две большие группы: теодолитные ходы и полигонометрические ходы.

В теодолитных ходах горизонтальные углы измеряют с ошибкой не более 30"; относительная ошибка измерения расстояний m_S/S колеблется от 1/1000 до 1/3000.

В полигонометрических ходах горизонтальные углы измеряют с ошибкой от 0.4" до 10", а относительная ошибка измерения расстояний m_S/S бывает от 1/5000 до 1/300 000. По точности измерений полигонометрические ходы делятся на два разряда и четыре класса (см. раздел 7.1).

Каждый определяемый пункт линейно-углового хода имеет две координаты X и Y, которые являются неизвестными и которые нужно найти. Общее количество пунктов в ходе обозначим через n, тогда количество неизвестных будет 2 * (n - 2), так как у двух пунктов (исходных начального и конечного) координаты известны. Для нахождения 2 * (n - 2) неизвестных достаточно выполнить 2 * (n - 2) измерений.

Подсчитаем, сколько измерений выполняется в разомкнутом линейно-угловом ходе: на n пунктах измерено n углов - по одному на каждом пункте, измерены также (n - 1) сторон хода, всего получается (2 * n - 1) измерений (рис.2.18).

Разность между количеством выполненных измерений и количеством необходимых измерений равна:

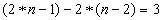(2.65)

то-есть, три измерения являются избыточными: это угол на предпоследнем пункте хода, угол на последнем пункте хода и последняя сторона хода. Но тем не менее, эти измерения выполнены, и их необходимо использовать при вычислении координат пунктов хода.

В геодезических построениях каждое избыточное измерение порождает какое-либо условие, поэтому количество условий равно количеству избыточных измерений; в разомкнутом линейно-угловом ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.

Условие дирекционных углов. Вычислим последовательно дирекционные углы всех сторон хода, используя формулу передачи дирекционного угла на последующую сторону хода:

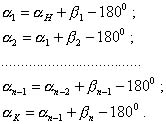(2.66)

Сложим эти равенства и получим:

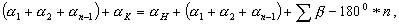
откуда
и 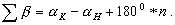(2.67)

Это - математическая запись первого геометрического условия в разомкнутом линейно-угловом ходе. Для правых углов поворота оно запишется так:

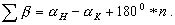(2.68)

Сумма углов, подсчитанная по формулам (2.67) и (2.68), называется теоретической суммой углов хода. Сумма измеренных углов вследствие ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую f_β:

(2.69)

Допустимое значение угловой невязки можно рассматривать как предельную ошибку суммы измеренных углов:

(2.70)

Используем известную формулу из теории ошибок для нахождения средней квадратической ошибки функции в виде суммы аргументов (раздел 1.11.2):

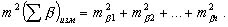(2.71)

При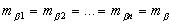
получим
или (2.72)

После подстановки (2.72) в (2.70) получаем:

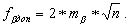(2.73)

Для теодолитных ходов m_β = 30", поэтому:

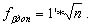(2.74)

Одним из этапов уравнивания является введение поправок в измеренные величины с целью приведения их в соответствие с геометрическими условиями. Обозначим поправку в измеренный угол V_β и запишем условие:

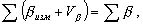
откуда следует, что:

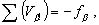(2.75)

то-есть, поправки в углы следует выбрать так, чтобы их сумма была равна угловой невязке с противоположным знаком.

В уравнении (2.75) n неизвестных, и для его решения необходимо наложить на поправки V_β (n-1) дополнительных условий; наиболее простым вариантом таких условий будет:

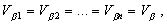(2.76)

то-есть, все поправки в измеренные углы одинаковы. В этом случае решение уравнения (2.75) получается в виде:

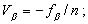(2.77)

это означает, что угловая невязка f_β распределяется с обратным знаком поровну во все измеренные углы.

Исправленные значения углов вычисляются по формуле:

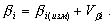(2.78)

По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем прави льности обработки угловых измерений.

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔX_i и ΔY_i. Координаты пунктов хода получим по формулам:

(2.79)

Сложим эти равенства и получим для приращений ΔX_i:

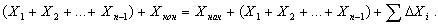
После приведения подобных имеем:

или

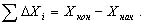(2.80)

Аналогичная формула для суммы приращений ΔY имеет вид:

(2.81)

Получились еще два условия (2.80) и (2.81), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон и упрощенного способа распределения угловой невязки суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам; возникают так называемые координатные невязки хода:

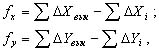(2.82)

по которым вычисляют абсолютную невязку хода:

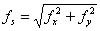(2.83)

и затем относительную невязку хода:

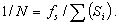(2.84)

Уравнивание приращений ΔX и ΔY выполняют следующим образом.

Сначала записывают суммы исправленных приращений:

и приравнивают их теоретическим суммам:

откуда следует, что:

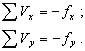(2.85)

В этих уравнениях по (n - 1) неизвестных и для их решения необходимо наложить на поправки V_X и V_Y дополнительные условия. На практике поправки в приращения координат вычисляют по формулам:

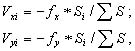(2.91)

которые соответствуют условию "поправки в приращения координат пропорциональны длинам сторон".

Рассмотренный способ обработки измерений в линейно-угловом ходе можно назвать способом последовательного распределения невязок; строгое уравнивание линейно-углового хода выполняется по методу наименьших квадратов.

После уравнивания одиночного линейно-углового хода ошибки положения его пунктов неодинаковы; они возрастают от начала и конца хода к его середине, и наибольшую ошибку положения имеет пункт в середине хода. В случае приближенного уравнивания эта ошибка оценивается половиной абсолютной невязки хода f_s. При строгом уравнивании хода производится сплошная оценка точности, то-есть вычисляются ошибки положения каждого пункта хода, ошибки дирекционных углов всех сторон хода, а также ошибки уравненных значений углов и сторон хода.

Дата добавления: 2014-01-06