Масштабы топографических карт

Топографические карты и планы

Понятие о барометрическом нивелировании

Барометрическое нивелирование основано на зависимости атмосферного давления от высоты точки над уровнем моря. Известно, что с увеличением высоты на 10 м давление падает примерно на 1 мм ртутного столба.

Приближенное значение превышения между точками 1 и 2 можно вычислить по формуле:

h = H₂ - H₁ = ΔH * (P₁ - P₂), (4.70)

где P₁ и P₂ - давление в первой и во второй точках;
ΔH - барометрическая ступень; значения ΔH выбирают из специальных таблиц.

Более точные формулы барометрического нивелирования получают, учитывая закономерности распределения плотности и температуры воздуха по высоте. Приведем полную формулу Лапласа:

h = K₀*(1 + α *t_m)*(1 + 0.378.e_m/P_m)* (1 + β*Cos2φf_m)*(1 + 2/R*H_m) *lg(P₁/P₂).

В этой формуле:
P₁, P₂ - давление воздуха на высоте H₁ и H₂ соответственно,
P_m - среднее значение давления,
H_m - среднее значение высоты,
t_m, e_m - среднее значение температуры и влажности воздуха,
f_m - среднее значение широты,
α - температурный коэффициент объемного расширения воздуха, равный 0.003665 град.^-1
β - коэффициент, равный 0.00265,
K₀ - коэффициент, равный 18400 при некоторых стандартных значениях давления воздуха и силы тяжести.

Известны и так называемые сокращенные барометрические формулы, в которых значения некоторых параметров состояния атмосферы приняты фиксированными; так в формуле М.В. Певцова:

h = N*(1 + α*tm) *lg(P₁/P₂),

где N = 18470, принято: e_m = 9 мм рт.ст., f_m = 55^o, H_m = 250 м, P_m = 740 мм рт.ст.

Точность барометрического нивелирования невысока; средняя квадратическая ошибка измерения превышения колеблется от 0.3 м в равнинных районах до 2 м и более в горных. Основные области применения барометрического нивелирования - геология и геофизика.

Масштабом называется степень уменьшения горизонтальных проложений линий местности при изображении их на плане, карте или аэроснимке. Различают численный и графические масштабы; к последним относятся линейный, поперечный и переходный масштабы.

Численный масштаб. Численный масштаб выражается в виде дроби, числитель которой равен единице, а в знаменателе стоит число, показывающее степень уменьшения горизонтальных проложений. На топографических картах численный масштаб подписывается внизу листа карты в виде 1:М, например, 1:10000. Если длина линии на карте равна s, то горизонтальное проложение S линии местности будет равно:

S = s * M. (5.1)

В нашей стране приняты следующие масштабы топографических карт: 1:1 000 000, 1:500 000, 1:200 000, 1:100 000, 1:50 000, 1:25 000, 1:10 000. Этот ряд масштабов называется стандартным. Раньше этот ряд включал масштабы 1:300 000, 1:5000 и 1:2000.

Линейный масштаб. Линейный масштаб - это графический масштаб; он строится в соответствии с численным масштабом карты в следующем порядке:

• проводится прямая линия и на ней несколько раз подряд откладывается отрезок a постоянной длины, называемый основанием масштаба (при длине основания a=2 см линейный масштаб называется нормальным); для масштаба 1:10 000 a соответствует 200 м,
• у конца первого отрезка ставится нуль,
• влево от нуля подписывают одно основание масштаба и делят его на 20 частей,
• вправо от нуля подписывают несколько оснований,
• параллельно основной прямой проводят еще одну прямую и между ними прочерчивают короткие штрихи (рис.5.1).

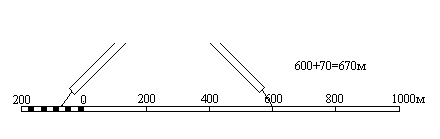
Рис.5.1

Линейный масштаб помещается внизу листа карты.

Чтобы измерить длину линии на карте, фиксируют ее раствором циркуля-измерителя, затем правую иглу ставят на целое основание так, чтобы левая игла находилась внутри первого основания. Считывают с масштаба два отсчета: N₁ - по правой игле и N₂ - по левой; длина линии равна сумме отсчетов

S = N₁ + N₂;

сложение отсчетов выполняют в уме.

Поперечный масштаб. Проведем прямую линию CD и отложим на ней несколько раз основание масштаба - отрезок a длиной 2 см (рис.5.2). В полученных точках восстановим перпендикуляры к линии CD; на крайних перпендикулярах отложим m раз вверх от линии CD отрезок постоянной длины и проведем линии, параллельные линии CD. Крайнее левое основание разделим на n равных частей. Соединим i-тую точку основания CA с (i-1)-й точкой линии BL; эти линии называются трансверсалями. Построенный таким образом масштаб называется поперечным.

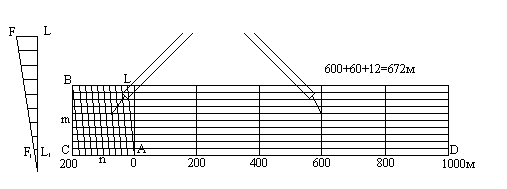
Рис.5.2

Если основание масштаба равно 2 см, то масштаб называется нормальным; если m = n = 10, то масштаб называется сотенным.

Наименьшее деление поперечного масштаба равно отрезку F₁L₁; на такую длину отличаются два соседних параллельно расположенных отрезка при движении вверх по трансверсали и по вертикальной линии. Теория поперечного масштаба заключается в выводе формулы цены его наименьшего деления.

Рассотрим два подобных треугольника AF₁ L₁ и AFL, из подобия которых следует:

(5.2)

откуда F₁L₁ = FL*(AL₁ / AL).

По построению FL = a/n и (AL₁ / AL) = 1/m. Подставим эти равенства в формулу (5.2) и получим:

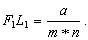(5.3)

При m = n = 10 имеем F₁L₁ = a/100, то-есть, у сотенного масштаба цена наименьшего деления равна одной сотой доле основания.

Порядок пользования поперечным масштабом:

• циркулем-измерителем зафиксировать длину линии на карте,
• одну ножку циркуля поставить на целое основание, а другую - на любую трансверсаль, при этом обе ножки циркуля должны располагаться на линии, параллельной линии CD,
• длина линии составляется из трех отсчетов: отсчет целых оснований, умноженный на цену основания, плюс отсчет делений левого основания, умноженный на цену деления левого основания, плюс отсчет делений вверх по трансверсали, умноженный на цену наименьшего деления масштаба. Точность измерения длины линий по поперечному масштабу оценивается половиной цены его наименьшего деления.

Переходный масштаб. Иногда в практике приходится пользоваться картой или аэроснимком, масштаб которых не является стандартным, например, 1:17500, то-есть, 2 см на карте соответствуют 350 м на местности; наименьшее деление нормального поперечного сотенного масштаба будет при этом 3.5 м. Оцифровка такого масштаба неудобна для практических работ, поэтому поступают следующим образом. Основание поперечного масштаба берут не 2 см, а расчитывают так, чтобы оно соответствовало круглому числу метров, например, 400 м. Длина основания в этом случае будет a = 400 м / 175 м = 2.28 см.

Если теперь построить поперечный масштаб с длиной основания a = 2.28 см, то одно деление левого основание будет соответствовать 40 м, а цена наименьшего деления будет равна 4 м.

Поперечный масштаб с дробным основанием называется переходным.

Точность масштаба. Карта или план - это графические документы. Принято считать, что точность графических построений оценивается величиной 0.1 мм. Длина горизонтального проложения линии местности, соответствующего на карте отрезку 0.1 мм, называется точностью масштаба. Практический смысл этого понятия заключается в том, что детали местности, имеющие размеры меньше точности масштаба, на карте в масштабе изобразить невозможно, и приходится применять так называемые внемасштабные условные знаки.

Кроме понятия "точность масштаба" существует понятие "точность плана". Точность плана показывает, с какой ошибкой нанесены на план или карту точечные объекты или четкие контуры. Точность плана оценивается в большинстве случаев величиной 0.5 мм; в нее входят ошибки всех процессов создания плана или карты, в том числе и ошибки графических построений.

Дата добавления: 2014-01-06