Аппроксимация и интерполяция

Программа для решения систем нелинейных уравнений методом Ньютона

INPUT X,Y,E

M: F=X^2+Y^2-1

G=X+Y

FX=2X: FY=2Y: GX=1: GY=1

I=FX*GY–FY*GX

IX=–F*GY+G*FY: IY=–G*FX+F*GX

DX=IX/I: DY=IY/I

X=X+DX, Y=Y+DY

PRINT X,Y,DX,DY,F,G

IF ABS(DX)>E OR ABS(DY)>E THEN GOTO M

PRINT X,Y,DX,DY

END

Лекция 8

Приближение одной функции к другой, как правило более простой, называют аппроксимацией. Аппроксимирующая функция должна выбираться в некотором заранее заданном классе, приемлемом для пользования функцией.

Существуют различные виды аппроксимации и при постановке задачи всегда должны быть заданы два объекта: класс функции, в котором выбирается аппроксимирующая функция и количественная характеристика близости аппроксимирующей функции, в результате аппроксимации эта характеристика должна стать достаточно малой, причем при постановке задачи ее величина должна быть определена заранее.

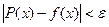
Примеры аппроксимирующих функций

1. Полиномиальная интерполяция. В этом случае заданы значения точек x_i, 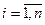и при этом заданы значения фугкции Р(x_i) в этих точках. Требуется найти алгебраический многочлен Q(х), который совпадал бы в точках x_i: Р(x_i)= Q(х_i), а в интервале точек x_i, 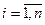разница этих полиномов не должна отличаться на большие величины.

x_i<x< x_i+1

|P(x)-Q(x)|<q

2. Среднеквадратичная точечная аппроксимация

	x1	x2	x3
x	1	6	y x yi i+1 y1 i -4
Y	2	7	0
	y1	y2	y3

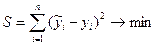
3. Равнополярная аппроксимация предполагает, что разница между аппроксимирующей функцией и аппроксимирующей между двумя точками была бы меньше возможной.

Дата добавления: 2014-01-06