Кодирование информации

Пример

Сводная таблица переводов целых чисел из одной системы счисления в другую

Рассмотрим десятичную, двоичную, восьмеричную и шестнадцатеричную системы счисления, которые применяются в компьютерах. Возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рис. 7.4:

Рис. 7. 4. Сводная схема переводов целых чисел из одной системы счисления в другую

На этом рисунке использованы следующие обозначения: в кружках записаны основания систем счисления; стрелки указывают направление перевода; номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 7.3.

Сводная таблица переводов целых чисел

Таблица 7. 3

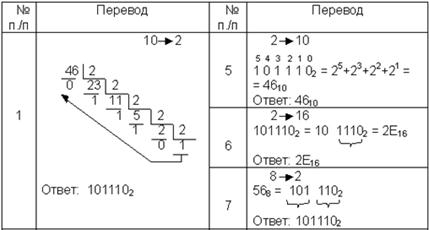
Продолжение табл. 7.3.

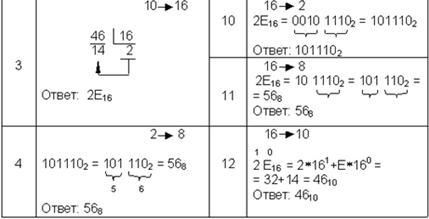
7.3. Арифметические операции,
выполняемые в позиционных системах счисления

В вычислительной технике наиболее часто выполняется операция сложения. Вычисления выполняются по следующим правилам:

- операция сложения выполняется поразрядно, начиная с младших разрядов в слагаемых;

- в каждом одноименном разряде слагаемых суммируются соответствующие цифры и перенос из предыдущего разряда суммы;

- если сумма цифр одноименных разрядов слагаемых и переноса меньше основания системы счисления, то перенос в следующий разряд равен нулю, если равна или больше — то равен единице.

В качестве примера рассмотрим арифметические операции в десятичной и двоичной системе счисления.

Арифметические операции над числами в двоичной системе счисления

Рассмотрим правила выполнения арифметических операций над однозначными числами. Представим е

Правила сложения	Правила вычитания	Правила умножения
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10	0 - 0 = 0 0 - 1 = -1 1 - 0 = 1 1 - 1 = 0	0 * 0 = 0 1 * 0 = 0 0 * 1 = 0 1 * 1 = 1

Сложение

Пример 1. Сложим числа 15 и 6.

Проверка. Преобразуем полученные суммы к десятичному виду: 101012 =
2⁴ + 2² + 2⁰ = 16+4+1=21.

Пример 2. Сложим числа 141,5 и 59,75.

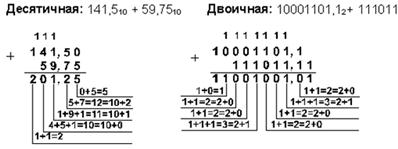
Проверка. Преобразуем полученные суммы к десятичному виду:

11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25

Вычитание

Пример 3. Вычтем единицу из чисел 10₂ и 100₂

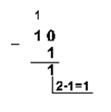
Пример 4. Вычтем число 59,75 из числа 201,25

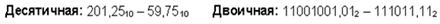
Проверка. Преобразуем полученные разности к десятичному виду:

10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^-1 = 141,5;

Умножение

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример 5. Перемножим числа 5 и 6.

Проверка. Преобразуем полученные произведения к десятичному виду:

11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;

Пример 6. Перемножим числа 115 и 51.

Проверка. Преобразуем полученные произведения к десятичному виду:

1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865;

В качестве наименьшей единицы измерения информации принят 1 бит, который соответствует одному разряду в двоичной системе счисления. Эта система лежит в основе архитектуры компьютеров. Для представления всего многообразия величин в компьютере объединяют несколько двоичных разрядов. Поэтому более крупными единицами измерения в компьютере являются: 1 байт = 8 бит; 1 Кбайт=2¹⁰ байт; 1 Мбайт = 2¹⁰ Кбайт; 1 Гбайт = 2¹⁰ Мбайт.

Поскольку информация в компьютере хранится в дискретной форме, для ее записи используется некоторый конечный набор знаков, называемый алфавитом. Очень часто в качестве алфавита используется таблица кодов, содержащая около 256 знаков. Каждому знаку соответствует числовой код. Этот код хранит образ соответствующего знака в памяти компьютера. Для понимания системы кодирования информации необходимо рассмотреть правила преобразования числовых кодов в различные системы счисления.

Наиболее популярна таблица кодов ASCII. Она состоит из 16 строк и 16 столбцов, пронумерованных от 0 до F в 16-ричной системе счисления. Например, в столбце 4 и строке D таблицы расположена заглавная буква М латинского алфавита. Таким образом, при записи текста с такой буквой, она будет храниться в памяти в виде кода 4D₁₆ или 77₁₀. Обычно последние 8 столбцов таблицы кодов содержат буквы национальных алфавитов, графические знаки. В большом количестве разновидностей таблицы кодов ASCII первая половина таблицы является неизменной, а вторая - переменной.

Таким образом, для хранения одного символа в ASCII-кодировке требуется 1 байт памяти компьютера. Однако 8-битовая кодировка является недостаточной для кодировки всех символов расширенных алфавитов. Все препятствия могут быть сняты при переходе на 16-битовую кодировку Unicode, допускающую 65536 кодовых комбинаций.

Числа кодируются особым образом.

Дата добавления: 2014-01-06