
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Никаких других формул в алгебре логики нет
|
|
|
|
7.15.
7.14.
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
Ответ
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
7.1. Используя Правило Счета, запишите первые 20 целых чисел в десятичной, двоичной, троичной, пятеричной и восьмеричной системах счисления.
7.2. Какие целые числа следуют за числами:
| а) 12; | е) 18; | п) F16; |
| б) 1012; | ж) 78; | м) 1F16; |
| в) 1112; | з) 378; | н) FF16; |
| г) 11112; | и) 1778; | о) 9AF916; |
| д) 1010112; | к) 77778; | п) CDEF16? |
7.3. Какие целые числа предшествуют числам:
| а) 102; | е) 108; | л) 1016; |
| б) 10102; | ж) 208; | м)2016; |
| в) 10002; | з) 1008; | н) 10016; |
| г) 100002; | и) 1108; | о) A1016; |
| д) 101002; | к) 10008; | п) 100016? |
7.4. Какой цифрой заканчивается четное двоичное число? Какой цифрой заканчивается нечетное двоичное число? Какими цифрами может заканчиваться четное троичное число?
7.5. Какое наибольшее десятичное число можно записать тремя цифрами:
а) в двоичной системе;
б) в восьмеричной системе;
в) в шестнадцатеричной системе?
7.6. В какой системе счисления справедливо следующее:
а) 20 + 25 = 100;
б) 22 + 44 = 110?
7.7. Десятичное число 59 эквивалентно числу 214 в некоторой другой системе счисления. Найдите основание этой системы.
7.8. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:
| а) 10110112; | е) 5178; | л) 1F16; |
| б) 101101112; | ж) 10108; | м) ABC16; |
| в) 0111000012; | з) 12348; | н) 101016; |
| г) 0,10001102; | и) 0,348; | о) 0,А416; |
| д) 110100,112; | к) 123,418; | п) 1DE,C816. |
7.9. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
а) 12510; б) 22910; в) 8810; г) 37,2510; д) 206,12510.
7.10. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
| а) 1001111110111,01112; | г) 1011110011100,112; |
| б) 1110101011,10111012; | д) 10111,11111011112; |
| в) 10111001,1011001112; | е) 1100010101,110012. |
7.11. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа:
а) 2СE16; б) 9F4016; в) ABCDE16; г) 1010,10116; д) 1ABC,9D16.
7.12. Выпишите целые числа:
а) от 1011012 до 1100002 в двоичной системе;
б) от 2023 до 10003 в троичной системе;
в) от 148 до 208 в восьмеричной системе;
г) от 2816 до 3016 в шестнадцатеричной системе.
Ответ
7.13. Для десятичных чисел 47 и 79 выполните цепочку переводов из одной системы счисления в другую:
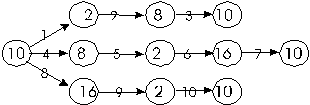
Ответ
7.14. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
7.15. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
7.16. Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:
| а) 10111012 и 11101112; | д) 378 и 758; | и) A16 и F16; |
| б) 1011,1012 и 101,0112; | е) 1658 и 378; | к) 1916 и C16; |
| в) 10112, 112 и 111,12; | ж) 7,58 и 14,68; | л) A,B16 и E,F16; |
| г) 10112, 11,12 и 1112; | з) 68, 178 и 78; | м) E16, 916 и F16. |
7.17. В каких системах счисления выполнены следующие сложения? Найдите основания каждой системы:
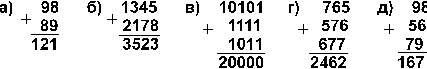
7.18. Найдите те подстановки десятичных цифр вместо букв, которые делают правильными выписанные результаты (разные цифры замещаются разными буквами):
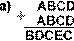
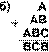
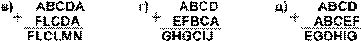
7.19. Вычтите:
| а) 1112 из 101002; | д) 158 из 208; | и) 1А16 из 3116; |
| б) 10,112 из 100,12; | е) 478 из 1028; | к) F9E16 из 2А3016; |
| в) 111,12 из 100102; | ж) 56,78 из 1018; | л) D,116 из B,9216; |
| г) 100012 из 1110,112; | з) 16,548 из 30,018; | м) ABC16 из 567816. |
7.20. Перемножьте числа, а затем проверьте результаты, выполнив соответствующие десятичные умножения:
| а) 1011012 и 1012; | д) 378 и 48; |
| б) 1111012 и 11,012; | е) 168 и 78; |
| в) 1011,112 и 101,12; | ж) 7,58 и 1,68; |
| г) 1012 и 1111,0012; | з) 6,258 и 7,128. |
Ответ
7.21. Разделите 100101102 на 10102 и проверьте результат, умножая делитель на частное.
7.22. Разделите 100110101002 на 11002 и затем выполните соответствующее десятичное и восьмеричное деление.
7.23. Вычислите значения выражений:
а) 2568 + 10110,12. (608 + 1210) - 1F16;
б) 1AD16 - 1001011002: 10102 + 2178;
в) 101010 + (10616 - 110111012) 128;
г) 10112. 11002: 148 + (1000002 - 408).
7.24. Расположите следующие числа в порядке возрастания:
а) 748, 1100102, 7010, 3816;
б) 6E16, 1428, 11010012, 10010;
в) 7778, 1011111112, 2FF16, 50010;
г) 10010, 11000002, 6016, 1418.
7.25. Прочитайте стихотворение. Переведите встречающиеся в нем числительные из двоичной системы счисления в десятичную.
| Необыкновенная девчонка А. Н. Стариков | |
| Ей было тысяча сто лет, Она в 101-ый класс ходила, В портфеле по сто книг носила – Все это правда, а не бред. Когда, пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато стоногий. | Она ловила каждый звук Своими десятью ушами, И десять загорелых рук Портфель и поводок держали. И десять темно-синих глаз Рассматривали мир привычно,… Но станет все совсем обычным, Когда поймете наш рассказ. |
7.26. За праздничным столом собрались 4 поколения одной семьи: дед, отец, сын и внук. Их возраст в различных системах счисления записывается так 88 лет, 66 лет, 44 года и 11 лет. Сколько им лет в десятичной системе счисления, если через год их возраст в тех системах счисления можно будет записать как 100?
ОТВЕТЫ К ЗАДАНИЯМ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
7.1. в) троичная: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201; г) пятеричная: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34.
7.2. а) 102; б) 1102; в) 10002; г) 100002; д) 1011002; е) 28; ж) 108; з) 408; и) 2008; к) 100008; л) 1016; м) 2016; н) 10016; о) 9AFA16; п) CDF016.
7.3. а) 12; б) 10012; в) 1112; г) 11112; д) 100112; е) 78; ж) 178; з) 778; и) 1078; к) 7778; л) F16; м) 1F16; н) FF16; о) A0F16; п) FFF16.
7.4. Четное двоичное число оканчивается цифрой 0, нечетное двоичное — цифрой 1, четное троичное — цифрами 0, 1 или 2.
7.5. а) 7; б) 511; в) 4091.
7.6. а) ни в какой; б) в шестеричной.
7.7. Основание 5.
7.8. а) 91; б) 183; в) 225; г) 35/64; д) 52,75; е) 335; ж) 520; з) 668; и) 7/16; к) 8333/64; л) 31; м) 2748; н) 4112; о) 41/64; п) 47825/32.
7.9. а) 11111012; 1758; 7D16; б) 111001012; 3458; E516; в) 10110002; 1308; 5816; г) 100101,012; 45,28; 25,416; д) 11001110,0012; 316,18; CE,216.
7.10. а) 11767,348; 13F7,716; б) 1653,5648; 3AB,BA16; в) 271,5478; B9,B3816; г) 13634,68; 179C,C16; д) 27,76748; 17,FBC16; е) 1425,628; 315,C816.
7.11. а) 10110011102; 13168; б) 10011111010000002; 1175008; в) 101010111100110111102; 25363368; г) 1000000010000,0001000000012; 10020,04018; д) 1101010111100,100111012; 15274,4728.
7.12. а) 1011012, 1011102, 1011112, 1100002; б) 2023, 2103, 2113, 2123, 2203, 2213, 2223, 10003; в) 148, 158, 168, 178, 208; г) 2816, 2916, 2A16, 2B16, 2C16, 2D16, 2E16, 2F16, 3016;
7.13. а) 4710 - 1011112 - 578 - 4710 - 578 - 1011112 - 2F16 - 4710 - 2F16 - 1011112 - 4710; б) 7910 - 10011112 - 1178 - 7910 - 1178 - 10011112 - 4F16 - 7910 - 4F16 - 10011112 - 7910.
| + | ||||||||||
| + | ||||||||||
| x | ||||||||||
| x | ||||||||||
7.16. а) 110101002; б) 10001,02; в) 10101,12; г) 11001,12; д) 1348; е) 2248; ж) 24,38; з) 348; и) 1916; к) 2516; л) 19,A16; м) 2616.
7.17. а) в 16-й; б) в 10-й; в) в 3-й; г) в 8-й; д) в 16-й.
7.18. в) А=9, B=4, C=5, D=3, F=1, L=0, M=7, N=8; г) A=3, B=6, C=2, D=5, E=9, F=7, G=1, H=0, I=4, J=8; д) A=9, B=3, C=4, D=2, E=1, F=8, G=0, H=7, I=6.
7.19. а) 11012; б) 1,112; в) 1010,12; г) -10,012; д) 38; е) 338; ж) 22,18; з) 11,258; и) 1716; к) 1A9216; л) -1,7E16; м) 4BBC16.
7.20. а) 111000012; б) 11000110,012; в) 1000000,1012; г) 1001011,1012; д) 1748; е) 1428; ж) 15.268; з) 55.22228.
7.21. 11112.
7.22. 11001112; 10310; 1478.
7.23. а) 149310; б) 54210; в) 142010; г) 1110.
7.24. а) 1100102, 3816, 748, 7010; б) 1428, 10010, 11010012, 6E16; в) 1011111112, 50010, 7778, 2FF16; г) 11000002, 6016, 1418, 10010.
7.25. 11002 = 1210; 1012 = 510; 1002 =410; 102 = 210.
7.26. Дед: 889 = 8010; Отец: 667 = 4810; Сын:445 = 2410; Внук: 112 = 310.
ГЛАВА 8. АЛГЕБРА ЛОГИКИ
8.1. Возникновение логики
как самостоятельной науки
Понятие логики как науки появилось ещё в XIX в., т.е. задолго до появления науки информатики и компьютеров. Элементы математической логики можно найти уже в работах древнегреческих философов.
Логику, основанную Аристотелем ( 384–322 до н. э. - крупнейший древнегреческий мыслитель ), принято называть формальной. Это название закрепилось за ней потому, что она возникла и развилась как наука о формах мышления.
В XVII в. Г. В. Лейбниц высказал идею о том, что рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам. Однако как самостоятельный раздел математики логика начала формироваться только с середины XIX в..
Для того чтобы рассуждать, человеку необходим какой-либо язык. Не удивительно, что математическая логика начиналась с анализа того, как говорят и пишут люди на естественных языках. Этот анализ привёл к тому, что выяснилось существование формулировок, которые невозможно разделить на истинные и ложные, но, тем не менее, выглядят осмысленным образом. Это приводило к возникновению парадоксов, в том числе в одной из фундаментальных наук математики. Тогда было решено создать искусственные формальные языки, лишённого «вольностей» языка естественного.

Рис. 8. 1. Джордж Буль – английский математик-самоучка
Джордж Буль (1815-1864г) по праву считается отцом математической логики (рис. 8.1). Его именем назван раздел математической логики – булева алгебра.
Буль изобрел своеобразную алгебру - систему обозначений и правил, применимую ко всевозможным объектам, от чисел до предложений. Пользуясь этой системой, он мог закодировать высказывания (утверждения, истинность или ложность которых требовалось доказать) с помощью символов своего языка, а затем манипулировать ими, подобно тому как в математике манипулируют числами.
Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому как утверждение может быть либо истинным, либо ложным.
А еще несколько десятилетий спустя, уже в ХХ столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.

Рис. 8. 2. Клод Шеннон – американский математик
В 1936 году выпускник Мичиганского университета Клод Шеннон (1916-2001г), которому был тогда 21 год, сумел ликвидировать разрыв между алгебраической теорией логики и ее практическим приложением (рис. 8.2).
Шеннон, имея два диплома бакалавра - по электротехнике и по математике, выполнял обязанности оператора на неуклюжем механическом вычислительном устройстве под названием "дифференциальный анализатор"
Постепенно у Шеннона стали вырисовываться контуры устройства компьютера. Если построить электрические цепи в соответствии с принципами булевой алгебры, то они могли бы выражать логические отношения, определять истинность утверждений, а также выполнять сложные вычисления. Свои идеи относительно связи между двоичным исчислением, булевой алгеброй и электрическими схемами Шеннон развил в докторской диссертации, опубликованной в 1938 году.
Применение в вычислительной технике и информатике алгебры логики
После изготовления первого компьютера стало ясно, что при его производстве возможно использование только цифровых технологий – ограничение сигналов связи единицей и нулём для большей надёжности и простоты архитектуры ПК. Благодаря своей бинарной природе, математическая логика получила широкое распространение в ВТ и информатике. Были созданы электронные эквиваленты логических функций, что позволило применять методы упрощения булевых выражений к упрощению электрической схемы. Кроме того, благодаря возможности нахождения исходной функции по таблице позволило сократить время поиска необходимой логической схемы.
В программировании логика незаменима как строгий язык и служит для описания сложных утверждений, значение которых может определить компьютер.
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1 - истина” и “0 - ложь”.
Из этого следует два вывода:
- Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных.
- На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов компьютера.
Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.
Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “ хлопанье ”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“ перебрасываться ”) из одного электрического состояния в другое и наоборот. Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 210 = 8192 триггеров. Современные микросхемы памяти содержат миллиарды триггеров.
8.2. Понятие “алгебры логики” как науки об общих операциях над логическими высказываниями[10]
Алгебра логики — это раздел математики, изучающийвысказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Так, например, предложение "Меню в программе – это список возможных вариантов" следует считать высказыванием, так как оно истинное. Предложение "Город Джакарта – столица Микронезии" тоже высказывание, так как оно ложное.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения "Какого цвета этот дом?" и "Эта тема скучна". Первое предложение вопросительное, а не повествовательное. Второе использует слишком неопределённое понятие "тема скучна".
Предложения типа "Рикки Мартин – самый популярный певец" не являются высказываниями, так как для выяснения его истинности или ложности нужны дополнительные сведения: о каком конкретно регионе, или о какой группе людей идет речь. Такие предложения называются высказывательными формами.
Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным. Часто трудно установить истинность высказывания. Так, например, высказывание "Численность жителей города Красноярска составляет 961 тыс. чел" может быть одновременно истинным и ложным. Ложным — так как указанное значение неточное и вообще не является постоянным. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если..., то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными. Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Зимой люди катаются на коньках", а через В — высказывание "Зимой люди катаются на лыжах".
Тогда составное высказывание "Зимой люди катаются на коньках и на лыжах" можно кратко записать как А и В. Здесь "и" — логическая связка, А, В — логические переменные, которые мoгут принимать только два значения — "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение. Базовыми являются пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция. Каждую логическую операцию можно иллюстрировать таблицей истинности.
Таблица истинности это табличное представление логической операции, в котором перечислены все возможные сочетания значений истинности входных операндов вместе со значением истинности выходного результата операции для каждого из этих сочетаний.
НЕ. Операция, выражаемая словом " НЕ ", называется отрицанием и обозначается чертой над высказыванием (или знаком 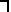 ). Высказывание
). Высказывание 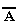 истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" (
истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" (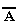 ). Таблица истинности логической операции " не " приведена в табл. 8.1.
). Таблица истинности логической операции " не " приведена в табл. 8.1.
Таблица истинности логического отрицания "НЕ"
Таблица 8. 1
| x | 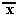
|
И. Операция, выражаемая связкой " И ", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой ". " (может также обозначаться знаками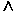 или *). Высказывание А . и В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание " 10 делится на 2 и 5 больше 3 " истинно, а высказывания " 10 делится на 2 и 5 не больше 3" — ложны. Таблица истинности логической операции " и " приведена в табл. 8.2.
или *). Высказывание А . и В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание " 10 делится на 2 и 5 больше 3 " истинно, а высказывания " 10 делится на 2 и 5 не больше 3" — ложны. Таблица истинности логической операции " и " приведена в табл. 8.2.
Таблица истинности логического умножения (конъюнкции) " И "
Таблица 8. 2
| Х | У | Х^У |
ИЛИ. Операция, выражаемая связкой "ИЛИ" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание " 10 не делится на 2 или 5 не больше 3 " ложно, а высказывания "10 делится на 2 или 5 больше 3", — истинны. Таблица истинности логической операции " или " приведена в табл. 8.3.
Таблица истинности логического сложения (дизъюнкции) " ИЛИ "
Таблица 8. 3
| Х | У | ХVУ |
ЕСЛИ-ТО. Операция, выражаемая связками "если..., то", "из... следует", "... влечет...", называется импликацией (лат. implico — тесно связаны) и обозначается знаком 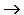 или
или 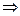 . Высказывание
. Высказывание 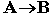 ложно тогда и только тогда, когда А истинно, а В ложно. Таблица истинности логической операции " импликация " приведена в табл. 8.4.
ложно тогда и только тогда, когда А истинно, а В ложно. Таблица истинности логической операции " импликация " приведена в табл. 8.4.
Таблица истинности импликации "ЕСЛИ-ТО "
Таблица 8. 4
| х | у | х—›у |
В обычной речи связка "если..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность.
РАВНОСИЛЬНО. Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "... равносильно...", называется эквиваленцией или двойной импликацией и обозначается знаком 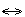 или ~. или ÛВысказывание
или ~. или ÛВысказывание 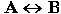 истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 3 - истино, а высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 5" - ложно. Таблица истинности логической операции " эквиваленции " приведена в табл. 8.5.
истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 3 - истино, а высказывание "24 делится на 6 тогда и только тогда, когда 24 делится на 5" - ложно. Таблица истинности логической операции " эквиваленции " приведена в табл. 8.5.
Таблица истинности эквиваленция, связка "Тогда и только тогда" Таблица 8. 5
| х | у | х‹—›у |
Импликацию можно выразить через дизъюнкцию и отрицание:
А 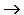 В =
В = 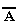 v В.
v В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А 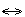 В = (
В = (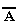 v В) . (
v В) . (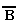 v А).
v А).
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции — дизъюнкция ("или") и в последнюю очередь — импликация.
8.3. логическая формул.
законы алгебрЫ логики
Логические формулы
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы.
Если А и В — формулы, то 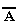 , А . В, А v В, А
, А . В, А v В, А 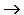 B, А
B, А 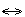 В — формулы.
В — формулы.
В качестве примера рассмотрим высказывание " Если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог ". Это высказывание формализуется в виде (A v B) 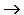 C.
C.
Как показывает анализ формулы (A v B) 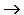 C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v 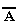 , соответствующая высказыванию " Этот треугольник прямоугольный или косоугольный ". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
, соответствующая высказыванию " Этот треугольник прямоугольный или косоугольный ". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
В качестве другого примера рассмотрим формулу А * 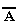 , которой соответствует, например, высказывание " Катя самая высокая девочка в классе, и в классе есть девочки выше Кати ". Очевидно, что эта формула ложна, так как либо А, либо
, которой соответствует, например, высказывание " Катя самая высокая девочка в классе, и в классе есть девочки выше Кати ". Очевидно, что эта формула ложна, так как либо А, либо 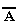 обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" или символом "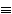 " Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Основные законы алгебры логики
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений (табл. 8.6):
Основные законы алгебры логики
Таблица 8. 6
| Закон | Для ИЛИ | Для И |
| Переместительный | 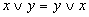
| 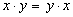
|
| Сочетательный | 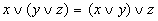
| 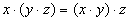
|
| Распределительный | 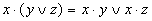
| 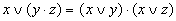
|
| Правила де Моргана | 
| 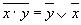
|
| Идемпотенции | 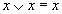
| 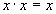
|
| Поглощения | 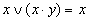
| 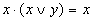
|
| Склеивания | 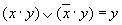
| 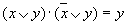
|
| Операция переменной с ее инверсией | 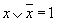
| 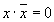
|
| Операция с константами | 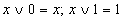
| 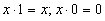
|
| Двойного отрицания | 
|
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1333; Нарушение авторских прав?; Мы поможем в написании вашей работы!