Алгоритм и его свойства

Каждый из нас постоянно встречается с множеством задач от самых простых и хорошо известных до очень сложных. Для многих задач существуют определенные правила (инструкции, предписания), объясняющие исполнителю, как решать данную задачу. Эти правила человек может изучить заранее или сформулировать сам в процессе решения задачи. Такие правила принято называть алгоритмами.

Алгоритм – это процедура, которая позволяет путем выполнения последовательности элементарных шагов получить однозначный результат или за конечное число шагов прийти к выводу о том, что решения не существует. Это точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к исходному результату, – понятное и точное предписание (указание) исполнителю совершить определенную последовательность действий, направленных на достижение указанной цели или решение поставленной задачи.

В качестве примера можно привести алгоритм прыжка в длину с разбега: разбег – отталкивание – полет – приземление. Из примера видно, что последовательность этапов прыжка в длину поменять местами невозможно, так как она разбита на элементарные фазы. В обычной жизни с алгоритмом решения какой-либо задачи мы можем столкнуться, например, при изготовлении различных кулинарных изделий и т. д.

Слово «алгоритм» происходит от «algorithmi» – латинской формы написания имени великого математика IX в. аль-Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмами и понимали только правила выполнения четырех арифметических действий над многозначными числами. В дальнейшем это понятие стали использовать вообще для обозначения последовательности действий, приводящих к решению поставленной задачи.

Любой алгоритм обладает рядом свойств:

1. Дискретность алгоритма. Процесс решения задачи, определяемый алгоритмом, расчленен на отдельные элементарные действия и соответственно алгоритм представляет последовательность указаний, команд, определяющих порядок выполнения шагов процесса.

2. Определенность алгоритма. Каждая команда алгоритма должна быть понятна исполнителю, не оставлять места для ее неоднозначного толкования и неопределенного исполнения. Описание алгоритма должно быть таким, чтобы его мог выполнить любой грамотный пользователь.

3. Результативность алгоритма. Выполнение алгоритма должно приводить к получению определенного результата после конечного числа шагов.

4. Массовость алгоритма. Каждый алгоритм, разработанный для решения некоторой задачи, должен быть применим для решения задач этого типа при всех допустимых значениях исходных данных.

Выполняя алгоритм, исполнитель может не вникать в смысл того, что он делает, и вместе с тем получать нужный результат. В таком случае говорят, что исполнитель действует формально, т. е. отвлекается от содержания поставленной задачи и только строго выполняет некоторые правила, инструкции.

Это очень важная особенность алгоритмов. Наличие алгоритма формализовало процесс, исключило рассуждения. Если обратиться к примерам других алгоритмов, то можно увидеть, что и они позволяют исполнителю действовать формально. Таким образом, создание алгоритма дает возможность решать задачу формально, механически исполняя команды алгоритма в указанной последовательности.

Построение алгоритма для решения задачи из какой-либо области требует от человека глубоких знаний в этой области, бывает связано с тщательным анализом поставленной задачи, сложными, иногда очень громоздкими рассуждениями. На поиски алгоритма решения некоторых задач ученые затрачивают многие годы. Но когда алгоритм создан, решение задачи по готовому алгоритму уже не требует каких-либо рассуждений и сводится только к строгому выполнению команд алгоритма.

В этом случае исполнение алгоритма можно поручить не человеку, а машине. Действительно, простейшие операции, на которые при создании алгоритма расчленяется процесс решения задачи, может реализовать и машина, специально созданная для выполнения отдельных команд алгоритма и выполняющая их в последовательности, указанной в алгоритме. Это положение и лежит в основе работы автоматических устройств, автоматизации деятельности человека.

На примере квадратного уравнения рассмотрим процесс создания алгоритма.

Пусть есть квадратное уравнение:

ax2 + bx + c = 0

1. Вычислим значение дискриминанта:

D = b2– 4ac

2. Если значение дискриминанта больше или равно нулю, то вычисляем корни уравнения:

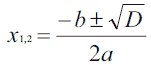
3. Если дискриминант меньше нуля, то уравнение действительных корней не имеет.

Каждое указание алгоритма предписывает исполнителю выполнить одно конкретное законченное действие. Исполнитель не может перейти к выполнению следующей операции, не закончив полностью выполнения предыдущей. Предписания алгоритма надо выполнять последовательно, одно за другим, в соответствии с указанным порядком их записи. Выполнение всех предписаний гарантирует правильное решение задачи. Данный алгоритм будет понятен исполнителю, умеющему работать с циркулем и знающему, что такое поставить ножку циркуля, провести окружность и т. д.

Анализ примеров различных алгоритмов показывает, что запись алгоритма распадается на отдельные указания исполнителю выполнить некоторое законченное действие. Каждое такое указание называется командой. Команды алгоритма выполняются одна за другой. После каждого шага исполнения алгоритма точно известно, какая команда должна выполняться следующей. Поочередное выполнение команд алгоритма за конечное число шагов приводит к решению задачи, к достижению цели.

Алгоритм может быть описан следующими способами:

• Словесно-формульное описание алгоритма, т. е. описание алгоритма с помощью слов или формул. Например, кулинарный рецепт.

• Графическое описание алгоритма, т. е. описание с помощью схем.

Схема алгоритма представляет собой систему связанных геометрических фигур. Каждая фигура обозначает один этап процесса решения задачи и называется блоком. Порядок выполнения этапов указывается стрелками, соединяющими блоки.

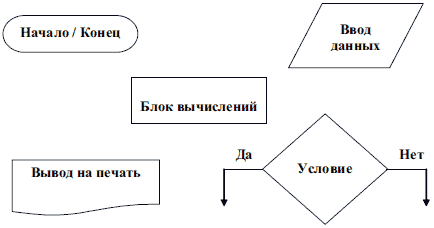
• Описание алгоритма на алгоритмическом языке.

Алгоритмический язык – это средство для записи алгоритмов в аналитическом виде, промежуточном между записью алгоритма на естественном языке и записью на языке ЭВМ (языке программирования).

• Описание алгоритма на языке программирования.

Выделяют следующие виды алгоритмов:

– Линейный;

– Разветвляющийся;

– Циклический.

Линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно.

Блок-схема нахождения периметра прямоугольного треугольника при известных длинах его катетов имеет следующий вид (рис. 8.1):

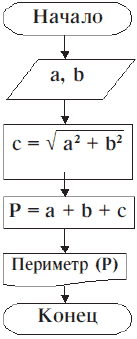
Рисунок 8.1. Блок-схема линейного алгоритма

Разветвляющийся алгоритм – это такой алгоритм, в котором выбирается один из нескольких возможных путей вычислительного процесса. Каждый подобный путь называется ветвью алгоритма. Признаком разветвляющегося алгоритма является наличие условия.

Блок-схема алгоритма решения квадратного уравнения выглядит следующим образом (рис. 8.2):

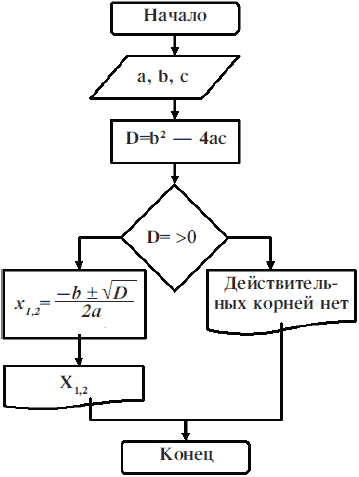
Рисунок 8.2. Блок-схема разветвляющегося алгоритма

Циклическим называют такой алгоритм, в котором получение результата обеспечивается многократным выполнением одних и тех же операций.

Задача № 3. Построить блок-схему возведения числа a в степень n (рис. 8.3).

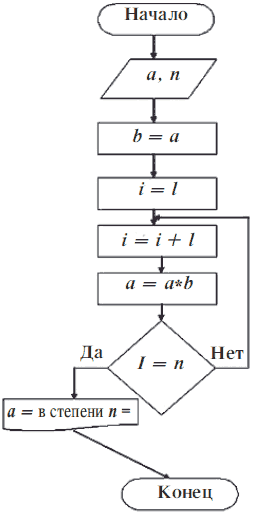
Рисунок 8.3. Блок-схема циклического алгоритма

Дата добавления: 2014-01-06