Червячные передачи

Трение

Пример выполнения чертежа зубчатого колеса (рис. 4.9).

Рис. 4.9

Трение – это совокупность явлений, возникающих в месте контакта двух тел, которые препятствуют их любому относительному движению.

Различают два вида трения: трение покоя (нет относительного движения тел); трение движения (есть относительное движение тел). Трение движения разделяется на трение скольжения и трение качения.

Сила трения – это сила, препятствующая относительному перемещению двух тел при трении. Между силой трения F и нормальной составляющей реакций на внешнее воздействие N существует зависимость

F = f* N, (4.18)

где f – коэффициент трения, определяемый опытным путем и зависящий от условий контакта тел.

Вы наверняка замечали, что сдвинуть груз с места труднее, чем двигать его после трогания с места. Поэтому различают силу трения покоя Fп и силу трения движения F.

Соответственно, следует различать коэффициент трения покоя

f _п = Fп/ N (4.19)

и коэффициент трения движения

f = F/ N (4.20)

Как правило f _п > f

Рассмотрим перемещение груза по горизонтальной (рис.4.10, а) и наклонной (рис.4.10, б, в) плоскостям.

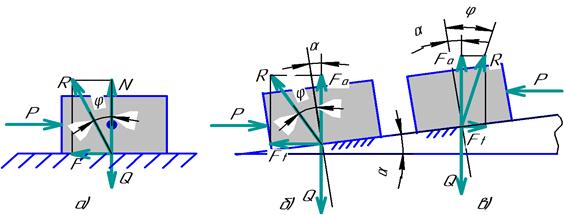
Рис. 4.10

Из рис.4.10, а) видим, что сила трения F отклоняет реакцию N на угол φ. Чтобы передвинуть груз надо приложить силу P ≥ F.

f = F/ N = tq φ. φ = arctq(f) (4.21)

– называется углом трения. При перемещении груза по наклонной плоскости (рис.4.10, б, в) реакцию F_а = Q отклоняет не только сила трения, но и составляющая силы тяжести, вызванная наклоном груза. В результате возникает сила сопротивления F_t = F_a*tq(φ + α) – при движении вверх; F_t = F_a*tq(φ - α) – при движении вниз.

Из рисунка 4.10, в) видим, что при отсутствии внешней силы P, пока угол трения φ > α груз не будет самопроизвольно перемещаться вниз. Условие φ > α называется условием самоторможения. При φ = α груз находится в состоянии безразличного равновесия.

Коэффициент трения скольжения зависит от многих факторов: материалов тел; вида и характера смазки; конфигурации тел; шероховатости контактирующих поверхностей и др. С учетом этих факторов общее понятие – коэффициент трения, заменяют понятием – приведенный коэффициент трения. А в формулах заменяют f = tq φ на f ' = tq φ', где φ' – приведенный угол трения.

Трение качения

При качении круглого тела по поверхности, из за деформации контактирующих тел, нормальная составляющая сил N смещается в сторону движения на величину k (рис.4.11), называемую коэффициентом трения качения и имеющую размерность см. При этом возникает момент трения равный

T_k = N*k (4.22)

Рис. 4.11

Для стального колеса, катящегося по рельсу k ≈ 0,005 см; для ролика или шарика, катящегося по закаленной дорожке подшипника качения,

k = 0,0005…0,001 см.

В механизмах и машинах потери на трение качения значительно меньше, чем на трение скольжения.

Поэтому, там, где это возможно, заменяют трение скольжения на трение качения. Например, в некоторых кулачковых механизмах, чтобы убрать трение скольжения толкателя по кулачку, на конце толкателя устанавливают ролик.

Приведенные выше понятия и формулы нужны при расчете червячных передач; фрикционных передач и механизмов; резьбовых соединений и др.

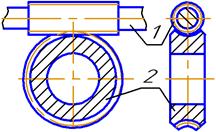Червячные передачи (рис. 4.12) относятся к числу зубчато-винтовых, имеющих характерные черты зубчатых и винтовых передач. Они состоят из червяка 1 и червячного колеса 2. Червяк представляет собой винт с резьбой близкой к трапецеидальной. Червячное колесо – это косозубое цилиндрическое колесо, особенностью которого является огибание зубьями колеса части

Рис. 4.12 окружности червяка. У червяка нет зубьев, у него есть винтовые нарезки (винтовые линии). Количество винтовых линий (при взгляде с торца червяка) называется числом заходов червяка z₁. В червячных редукторах обычно z₁ = 1 или 2.

Передаточное отношение равно u = z₂/ z₁, где z₂ – число зубьев червячного колеса.

Основные достоинства червячных передач: большое передаточное число при малых габаритах передачи (в стандартных редукторах u = 8…100); возможность самоторможения (используется в грузоподъемных механизмах); плавность и бесшумность работы.

Недостатки: низкий КПД (0,7…0,85); необходимость применения для колеса дорогостоящих антифрикционных материалов.

Материалы червячных передач: червяк стальной закаленный и желательно шлифованный; червячное колесо или его венец – бронзовые, в крупногабаритных передачах – чугунные.

На рис. 4.13 показана развертка винтовой линии двухзаходного червяка по делительной окружности. На рисунке приняты обозначения: p – шаг червяка (p = π*m); p_x – ход винтовой линии; d – делительный диаметр червяка; γ – делительный угол подъема витка червяка.

Очевидно соотношение p_x = p* z₁ = π* m* z₁

Видим p_x/ (πd) = tq γ, отсюда, заменяя p_x = π* m* z₁, получаем

d = m* z₁/ tq γ = q* m.

Параметр q = z₁/tq γ (4.23)

называется коэффициентом диаметра червяка. Эта

Рис. 4.13 величина стандартизована.

ГОСТ 2144-76 рекомендует ряд значений q в сочетании с рядом модулей.

Остальные параметры (элементы) передачи определяются аналогично зубчатым передачам.

d_a1 = d₁ + 2m = m*(q +2); d_f1 = d₁ – 2,4m = m*(q – 2,4); длину нарезанной части червяка b₁ принимают b₁ ≥ (11 + 0,06 z₂).

d₂ = m* z₂; d_a2 = d₂ + 2 m = m*(z₂ + 2); d_f2 = d₂ – 2,4m = m*(z₂ – 2,4); наибольший диаметр червячного колеса определяют по формуле

d_am2 ≤ d_a2 + 6 m/(z₁ +2); ширина венца колеса b₂ ≤ 0,75 d_a1.

Коэффициент полезного действия червячного редуктора с учетом потерь в зацеплении и в опорах определяется по формуле

η = (0,95…0,96)*tq γ/[tq(γ + φ')], (4.24)

где φ' – приведенный угол трения. КПД возрастает с увеличением числа заходов червяка, поскольку увеличивается γ. Приведенный угол трения очень сильно зависит от скорости скольжения

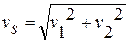, (4.25)

где v₁ = 0,5ω₁*d₁*10 ^–3 и v₂ = 0,5ω₂*d₂*10 ^–3 – окружные скорости червяка и колеса, м/с; ω₁ и ω₂ – угловые скорости червяка и колеса, рад/с.

При увеличении скорости скольжения от 0,01 м/с до 15 м/с приведенный угол трения уменьшается от 6⁰ до 1⁰, а следовательно повышается КПД.

В червячной передаче наиболее слабым звеном является колесо, поэтому прочностные расчеты проводят именно червячного колеса. Расчеты выполняются в такой последовательности.

Известно: Т₂; u = z₂/ z₁; принимаете сами z₁ и q; выбираете материал колеса и по рекомендациям или задавшись коэффициентом запаса прочности определяете [σ]_H.

Определяете межосевое расстояние по формуле

, (4.26)

где Т₂ – крутящий момент на валу колеса, Н*мм (определяется из кинематического расчета).

Учитывая, что a_w = (d₁ + d₂) / 2 = m*(q + z₂)/2, (4.27)

m = 2 a_w/*(q + z₂) (4.28)

Затем определяете все остальные параметры (элементы) передачи по формулам, приведенным выше.

В заключение проводим проверку выполнения условия прочности на изгиб

σ_F = 1,5Y_F*K_Fβ*K_Fv*cos γ*T₂/(d₁*d₂*m) ≤ [σ]_F (4.29)

Все коэффициенты и допустимое напряжение берем из литературы.

В случае не выполнения условия прочности, определяем модуль по формуле

(4.30)

Дата добавления: 2014-01-06