Обозначения

Входные сигналы – g(t), их интегральные преобразования G(·),

Сигналы на выходе x(t), y(t), их интегральные преобразования X(·), Y(·).

Символ дифференцирования

W(p) – дифференциальный полином разомкнутой САУ.

W(p)x(t)=0 – описание свободного движения разомкнутой САУ при заданных начальных условиях, например, x(0)=x_0.

Например, уравнение

может быть записано в виде

,

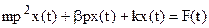или

.

Интегральные преобразования:

F(s) - преобразованная по Лапласу функция f(t);

F(jω) - преобразованная по Фурье функция f(t);

Передаточная функция W(s), передаточная функция замкнутой САУ Ф(s)

Частотная передаточная функция W((jω), разомкнутой САУ, частотная передаточная функция замкнутой системы Ф((jω).

Направление положительного отсчета углов на комплексной плоскости - против часовой стрелки.

1. Логарифмические частотные характеристики

Для решения практических задач широкое распространение получили графические методы с использованием амплитудных и фазовых частотных характеристик систем регулирования.

При построении амплитудных частотных характеристик оказывается удобным использовать логарифмические масштабы как по оси абсцисс (обычно - это ось частот), так и по оси ординат. Основание логарифма обычно выбирается равным десяти. Отрезок на оси частот, на котором значение частоты w изменяется в 10 раз, называется декадой. Декадаявляется линейным масштабом оси частот.

Логарифмические масштабы упрощают графическое изображение и анализ амплитудных частотных характеристик системы так как в этом случае амплитудные частотные характеристики систем могут быть с достаточной для инженерных расчетов точностью заменены асимптотами.

Поскольку амплитудная частотная характеристика системы - это произведение модулей передаточных функций звеньев, логарифмы амплитудных частотных характеристик отдельных звеньев системы суммируются. При построении логарифмической амплитудной частотной характеристики (ЛАЧХ) по оси ординат откладывают величину

L (ω)= LmA(ω) = 20lgA(ω)=20lg½W(jω)½, единицей измерения которой, является децибел.

В таблице приведены значения Lm для некоторых значений k:

Таблица 2.

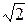
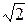
k	10^-2	10^-1	1/	1/2	1/						10^2
Lm (Дб)	-40	-20	-10	-6	-3

Изменению k на ±1 дБ соответствует увеличение модуля передаточной функции примерно на ±12%.

Отсюда могут быть получены и другие значения. Например, для k=5

20lg(5) = 20lg(10/2) = 20lg(10)-20lg(2)= 20-6 =14 дБ.

Логарифмировать можно только безразмерные величины. Поэтому когда говорят о логарифме lgA(w) полагают, что эта величина либо безразмерна, что случается, когда размерности входной и выходной величин совпадают

Поскольку аргументы отдельных звеньев при последовательном соединении суммируются, фазовые характеристики звеньев и систем строятся в линейном масштабе. При построении логарифмической фазовой частотной характеристики (ЛФЧХ) отсчет углов j идет по оси ординат в линейном масштабе в градусах, а по оси абсцисс частота w откладывается в логарифмическом масштабе.

Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза (w_с). Эта частота соответствует A(w_с)=1. Начало координат обычно помещают в точке w=1, хотя это и не обязательно.

Логарифмический масштаб по оси частот упрощает и изображение фазовых характеристик систем. Если нет логарифмической разметки оси частот, то, определив равномерный масштаб частот по декадам, для разметки оси частоты внутри декады можно воспользоваться шкалами рисунке.

В большинстве оказывается возможным и фазовые характеристики заменять асимптотами в виде отрезков прямых линий.

2. Передаточные функции типовых звеньев

Передаточные функции линейных звеньев могут быть представлены в виде дроби

,

где N(s) и L(s) – многочлены степеней n и m (n>m) по s.

Линейные звенья, в передаточные функции которых входят многочлены N(s) и L(s) со свободными членами отличными от нуля называют позиционными (или статическими). Обычно соответствующим выбором коэффициента k свободные члены делают равными единице. Тогда, в соответствие с теоремой о предельном значении, установившаяся реакция позиционных звеньев на единичный скачек 1(t) входного сигнала - h₁(t)=k, то есть в установившемся режиме сигналы на входе (g) и выходе (x) связаны равенством x=kg.

Дата добавления: 2014-01-06