Наименьших квадратов

Эмпирических формул методом

Определение коэффициентов

Нередко при обработке результатов наблюдений встречаются со следующей задачей: в итоге опыта получен ряд значений переменных x и y, однако характер функциональной зависимости между ними остается неизвестным. Требуется по полученным данным найти аналитическое выражение зависимости между ними. Формулы, полученные в результате решения задач подобного рода, называются эмпирическими.

Задача о построении эмпирической формулы состоит в следующем.

Пусть в результате экспериментов получены данные, представленные таблицей:

x1	x2	...	xk	...	xn
y1	y2	...	yk	...	yn

где х_i - значения аргумента, изменяющиеся с постоянным шагом и расположенные в порядке возрастания их значений, y_i - экспериментальные значения функции, соответствующие данным значениям аргументов.

Требуется найти эмпирическую формулу у=f(x_i,a₁,a₂,…a_m), где функция f зависит не только от значения аргумента х_i, но и от некоторых параметров a_j. Разности

f(x_i,a₁,a₂,…a_m)-y_i=e_i, (i=1,2,3,..m) (6.9)

называются отклонениями или погрешностями, где

x_i - числа из первой строки таблицы,

y_i - числа из второй строки данной таблицы,

f(x_i,a₁,a₂,…a_m) - значения функции при соответствующих значениях аргумента x_i.

Параметры a_j эмпирической формулы y=f(x,a₁,a₂,…a_m) необходимо подобрать таким образом, чтобы отклонения e_i оказались наименьшими. Наиболее распространенным критерием является критерий, лежащий в основе метода наименьших квадратов: параметры функции выбирают так, чтобы сумма квадратов отклонений оказалась минимальной:

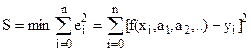(6.10)

Минимум функции находят приравнивая нулю частные производные по переменным параметрам а_j

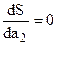, , … (6.11)

Полученные соотношения образуют систему уравнений, для определения коэффициентов a_i, для i=1,2,..,m.

Пусть функция f(x) является многочленом степени m, т.е.

f(x)=a₀x^m + a₁x^m-1 +...+a_ix^m-i +...+a_m-2x² a_m-1x + a_m, (a₀ не равно 0).

Задача ставится следующим образом: подобрать коэффициенты многочлена так, чтобы сумма квадратов отклонения для данного многочлена оказалась минимальной.

В случае m=1 имеем линейное приближение функции по методу наименьших квадратов, в случае m=2 - квадратичное приближение.

В случае линейной зависимости предполагается, что все точки лежат на некоторой прямой

y=a*x+b, (6.12)

где a и b - некоторые постоянные параметры, подлежащие определению. Для их нахождения требуется решить систему:

a*Sx_i² + b*Sxⁱ = Sxⁱ*yⁱ (6.13)

a*Sx_i + b*n =Sy_i

В случае квадратичной зависимости предполагается, что все точки лежат на некоторой параболе. В этом случае естественно предположить, что между ними существует квадратичная зависимость, т.е.

y=a*x²+b*x+c, (6.14)

где a, b, c - постоянные параметры, подлежащие определению. Они находятся из системы:

a*Sx_i ⁴+ b*Sx_i³ + c*Sx_i² = Sy_i*x_i²

a*Sx_i³ + b*Sx_i² + c*Sx_i =Sx_i*y_i (6.15)

a*Sx_i² + b*Sx_i + c*n =Sy_i

Решение системы осуществляется любым известным методом.

После того как найдены значения коэффициентов систем уравнений (6.13) и (6.15), вычисляют значения выражений (6.12) и (6.14) при заданных значениях аргументов. Каждое из полученных уравнений удовлетворяет условию (6.11).

Для выбора предпочтительной функции из двух также применяют метод наименьших квадратов. Для этой цели находят отклонения по формулам и квадраты этих отклонений для каждого метода (6.10). Предпочтительной будет та функция, для которой сумма квадратов отклонений будет наименьшая.

Дата добавления: 2014-01-06