Алгоритм табулирования функции

Табулирование функции – это вычисление ее значений по изменяющимся значениям аргумента функции.

Табулируют функцию, например, для построения ее графика, для поиска ее максимальных значений. Табулирование функции y = f(x) ведется на некотором интервале значений аргумента x € [х_н; х_к], с изменением значений аргумента на одинаковую величину ∆х, которую называют шагом изменения х.

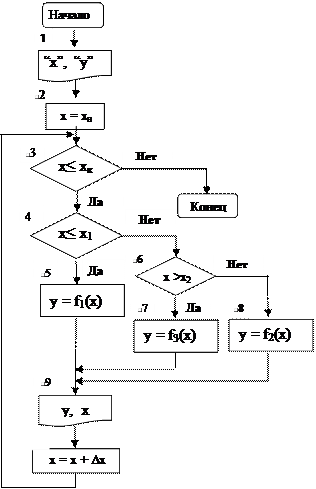Пример. Разработать алгоритм табулирования функции y, приведенной на стр. 44, на интервале значений х € [х_н; х_к], с шагом ∆х изменения аргумента. Блок-схема алгоритма решения этой задачи приведена на рис. 10.

Рис. 11. Блок-схема алгоритма табулирования функции

“Блок 1” обеспечивает печать заголовка таблицы, а блок 9 – строк таблицы, чтобы получить таблицу следующего вида:

x	y
хн	yн
х + ∆х	yн+1
x + 2∆х	yн+2
…	…
хк - ∆х	yк-1
xк	yк

“Блок 2”, “Блок 3” и “Блок 10” обеспечивают цикличность вычисления y в соответствии с изменением значения аргумента х от начального значения х_н до конечного значения х_к с шагом ∆х.

Алгоритм поиска экстремальных значений (max, min )

Перед началом подсчета необходимо предусмотреть переменные (например, max и min), куда будут помещаться значения функции, подходящие в качестве соответственно максимального и минимального значения. Начальными значениями этим переменным могут быть присвоены такие, которые с высокой вероятностью не соответствуют истинным, например:

max = -1Е+38 min =1Е+38

Суть алгоритма поиска экстремальных значений в том, что в процессе табулирования, после вычисления очередного значения функции его сравнивают со значением max и min. Если это значение больше max, то оно принимается в качестве max, а если рассматриваемое значение меньше min, то его принимают в качестве min. В итоге, после вычисления последнего значения функции в переменных max и min окажутся соответственно самое большое и самое маленькое из всех вычисленных значений функции.

На рис. 12 приведен пример алгоритма нахождения максимальных и минимальных значений функции при ее табулировании в соответствии с алгоритмом, представленным на рис. 11.

В заключение отметим некоторые правила построения блок-схем алгоритмов:

- должно рационально использоваться имеющееся на листе место;

- размещение блоков схемы должно, по возможности, отражать последовательность выполнения операций, полагая их следование сверху вниз;

- исходящая линия “Да” должна быть направлена вниз;

- исходящая линия “Нет”, как правило, должна идти вправо;

- входящие в блоки линии входа должны быть направлены сверху;

- исходящие линии тока должны быть направлены вниз.

Рис. 12. Нахождение минимума и максимума

Дата добавления: 2014-01-06