Гранные поверхности

Образование и приближенная классификация поверхностей

Лекция №3. Образование поверхностей. Гранные поверхности

В начертательной геометрии поверхность рассматривается как множество последовательных положений некоторой линии – образующей поверхности, перемещающейся в пространстве определенным образом по другой линии, которую называют направляющей.

Образующая поверхности в процессе движения может изменять свою форму. Одна и та же поверхность может быть образована перемещением различных линий.

Поверхности можно разбить на классы:

1) плоскости;

2) гранные поверхности;

3) линейчатые поверхности;

4) винтовые поверхности;

5) циклические поверхности;

6) поверхности вращения.

Плоскости

Плоскостью называется поверхность, полученная при движении прямой-образующей по прямой-направляющей. О ней достаточно подробно говорилось выше.

Гранные поверхности

Гранной называется поверхность, полученная при движении прямой-образующей по ломаной линии (направляющей). Об этих поверхностях расскажем более подробно ниже.

Линейчатые поверхности

Линейчатой поверхностью называется поверхность, которая описывается какой-либо прямой (образующей) при ее движении в пространстве по какому-нибудь закону.

В общем случае линейчатая поверхность может быть получена движением прямой линии по трем направляющим (рис. 3.1). В самом деле, если выделить на линейчатой поверхности три какие-либо линии а, b и c и принять их за направляющие, то движение образующей l определится единственным образом.

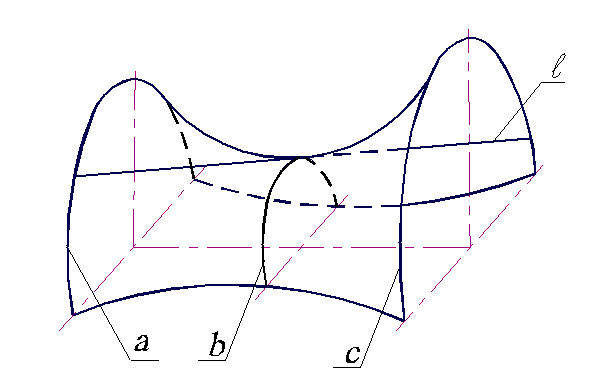
Рис. 3.1. Образование линейчатой поверхности.

Построение какой-либо точки на линейчатой поверхности производят при помощи ее образующей, проходящей через эту точку.

В зависимости от вида направляющих линий и характера движения образующей получаются различные типы линейчатых поверхностей.

Линейчатые поверхности с одной направляющей

Коническая поверхность образуется движением прямой l (образующей) по некоторой кривой m (направляющей) и имеющей неподвижную точку S (вершину) (рис. 3.2, а).

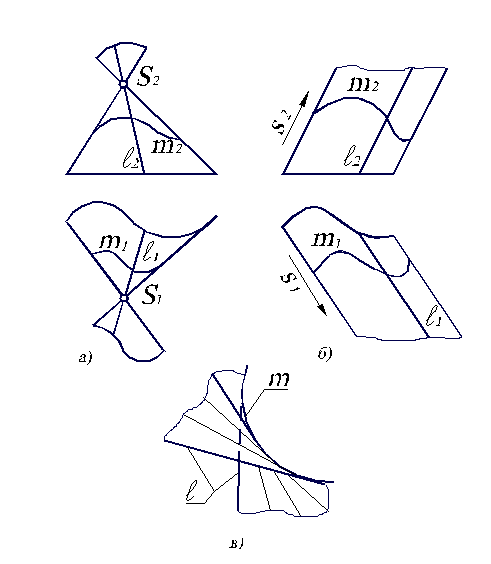
Рис. 3.2. Линейчатые поверхности с одной направляющей.

Цилиндрическая поверхность образуется движением прямой линии l (образующей) по некоторой кривой m (направляющей) и имеющей постоянное направление s (рис. 3.2, б).

Торс образуется движением прямолинейной образующей l, касающейся во всех своих положениях некоторой пространственной кривой m, называемой ребром возврата (рис. 3.2, в).

Линейчатые поверхности с двумя направляющими

Цилиндроид образуется движением прямолинейной образующей l по двум криволинейным направляющим а и b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма S (рис.3.3, а).

Рис. 3.3. Линейчатые поверхности с двумя направляющими

Коноид образуется движением прямолинейной образующей l по двум направляющим, из которых одна является кривой линией а, а другая прямой b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма S (рис.3.3, б).

Косая плоскость образуется движением прямолинейной образующей l по двум скрещивающимся прямолинейным направляющим а и b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма S (рис.3.3, в).

Линейчатые поверхности с тремя направляющими

Однополостный гиперболоид образуется вращением прямолинейной образующей l по трем криволинейным направляющим а, b и c (рис. 3.1).

.

Винтовые поверхности

Винтовой поверхностью называется поверхность, которую образует некоторая линия, совершающая винтовое движение.

Винтовым движением называют такое сложное движение, которое является результатом двух одновременных движений: вращательного и поступательного. При этом вращение происходит вокруг оси винта i, а поступательное – вдоль оси i.

Если отношение скоростей этих движений есть величина постоянная, то образуется поверхность с постоянным шагом; в противном случае - с переменным шагом.

Ходом винтовой поверхности называется линейное перемещение Р образующей l за один оборот (рис. 3.4). Каждая точка образующей l описывает при ее движении винтовые линии m – направляющие поверхности.

Рис. 3.4. Винтовые поверхности.

Если образующей винтовой поверхности является прямая линия, то поверхность называется линейчатой винтовой поверхностью или геликоидом. Геликоид называется прямым или наклонным в зависимости от того, перпендикулярна образующая к оси геликоида или нет (рис. 3.4).

Циклические поверхности

Циклической поверхностью называется поверхность, которая образовывается при произвольном движении окружности постоянного или переменного радиуса.

Различают два основных вида циклических поверхностей:

Каналовая поверхность образуется движением окружности m переменного радиуса, причем центр окружности О перемещается по заданной кривой l (направляющей), а ее плоскость остается перпендикулярной к этой кривой (рис.3.5, а).

Трубчатая поверхность отличается от каналовой только тем, что образующая ее окружность m имеет постоянный радиус(рис.3.5, б).

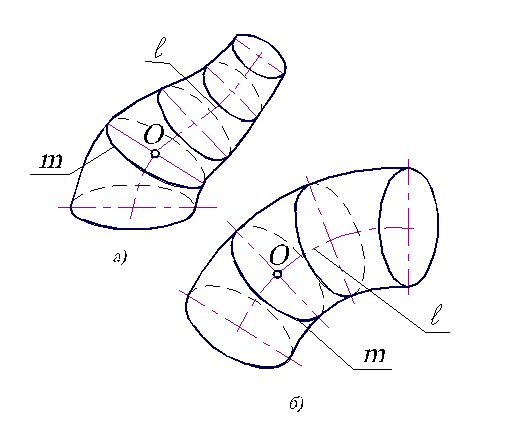
Рис. 3.5. Циклические поверхности.

Поверхности вращения

Поверхности вращения образуются при вращении некоторой произвольной линии вокруг оси. В этом случае образующей является указанная линия, а направляющей — окружность. Форма поверхности вращения определяется формой образующей.

Если образующей является прямая линия, а направляющей ломаная, получаем гранную поверхность. Когда образующая закреплена в одной точке, при движении по направляющей она вычерчивает пирамидальную поверхность (рис. 3.6, а). Если образующая перемещается параллельно какому-либо направлению, получаем призматическую поверхность (рис. 3.6, б).

В дальнейшем из всех гранных поверхностей рассмотрим лишь призматическую и пирамидальную.

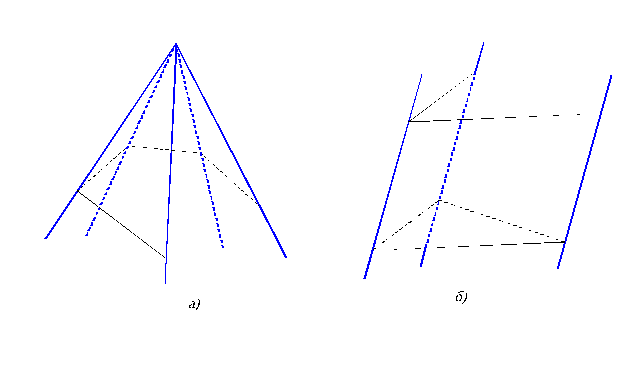
Рис.3.6. Образование гранных поверхностей.

Дата добавления: 2014-01-06