Методика массовых расчетов автономных солнечных электростанций

Для проведения расчетов параметров автономных солнечных электростанций для массовых заказчиков желательно иметь инженерные методы, позволяющие получать искомые оптимальные параметры более простыми способами без поиска экстремумов целевых функций. В основе таких расчетов могут быть различные эмпирические функции (например, функции уравнений линейной регрессии), графики и таблицы, описывающие зависимости оптимальных параметров от влияющих факторов. Получить такие зависимости можно путем описания движения оптимального параметра в области изменения влияющих на него факторов.

В таблице 5.1 приведены оптимальные параметры автономной системы электроснабжения удаленных сельских объектов на основе использования энергии солнечного излучения, а на рисунках 5.6 и 5.7 приведены графики этих параметров в зависимости от средней потребляемой мощности электроприемников и требуемой надежности электроснабжения /5, 6/.

Таблица 5.1

Расчетные параметры автономного энергетического комплекса

сезонно работающих объектов

Средняя нагрузка объекта, Вт	Площадь ФЭП (м^2) при вероятности энергообеспечения:	Емкость аккумуляторной батареи (А.ч) при вероятности энергообеспечения
	0,5	0,6	0,7	0,8	0,9	0,5	0,6	0,7	0,8	0,9
	22,3 28,0 33,0 38,5 43,5	26,0 32,5 38,5 44,7 51,0	29,0 35,8 42,5 49,3 56,7	31,2 38,3 46,0 53,5 61,0	35,5 44,5 53,0 62,0 71,0

Так как оптимальные размеры батареи фотоэлектрических преобразователей и емкость аккумуляторных батарей зависят от двух исходных параметров – средней нагрузки потребителя и надежности энергообеспечения (см. таблицу 5.1), то можно построить поверхности отклика этих параметров автономной системы электроснабжения (рисунки 5.8 и 5.9). Полученные поверхности отклика достаточно точно описываются уравнениями регрессии третьей степени.

Рисунок 5.6. Размеры батареи фотоэлектрических преобразователей

в зависимости от нагрузки и надежности энергообеспечения

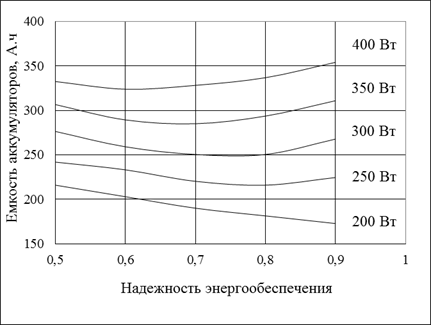
Рисунок 5.7. Емкость аккумуляторных батарей в зависимости от нагрузки и надежности энергообеспечения

Рисунок 5.8. Оптимальная площадь батареи ФЭП

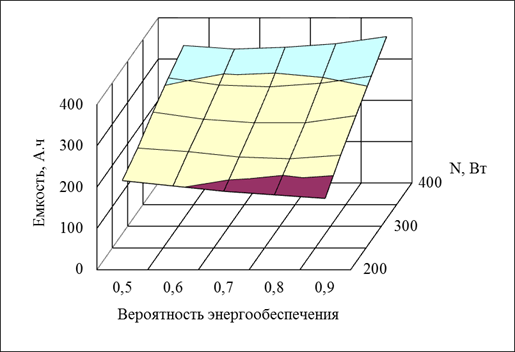
Рисунок 5.9. Оптимальная емкость аккумуляторной батареи

F = 0,066х₁ + 596х₂ + 0,168х₁х₂ – 0,0002х₁² – 894х₂² +

+ 1,9Е-07х₁³ + 435х₂³ – 131 (5.10)

С_А = 0,449х₁ – 370х₂ + 0,786х₁х₂ – 0,0013х₁² – 216х₂² +

+ 1,9Е-06х₁³ + 288х₂³ + 303 (5.11)

Здесь: х₁ – среднесуточная нагрузка, Вт;

х₂ – заданная вероятность энергообеспечения.

По полученным уравнениям регрессии можно проводить массовые расчеты параметров автономных солнечных электростанций на фотоэлектрических преобразователях солнечного излучения. В случае применения концентраторов солнечного излучения и систем слежения площадь батарей фотоэлектрических преобразователей уменьшается и определяется по формуле:

F_УТ = k_УТ F (5.12)

где F_УТ – уточненное значение площади батарей фотоэлектрических преобразователей, м²;

F – площадь батареи фотоэлектрических преобразователей по формуле (5.10), м²_;

k_УТ – коэффициент уточнения.

Значения коэффициентов уточнения площади батарей фотоэлектрических преобразователей приведены в таблице 5.2 /6/.

Таблица 5.2

Значения коэффициентов уточнения

Вариант	Коэффициент уточнения
1. Система точного слежения без концентраторов 2. Параболические концентраторы с периодическим слежением и коэффициентом концентрации: до 3; 3 – 5; больше 5. 3. Концентраторы первого порядка с системой точного слежения и коэффициентом концентрации: до 3; больше 3.	0,75   0,65 0,55 0,50   0,65 0,55

Дата добавления: 2014-01-06